الامتحانات التجريبية

بسم االله الرحمن الرحيم والصلاة والسلام على أشرف المخلوقين محمد سيد المرسلين وعلى آله وصحبه أجمعين أما بعد ٬ يستمر مسلسل الكتب المفهرسة ٬ بتقديم هذا العمل المتواضع وهو عبارة على 15 امتحان تجريبي مع الحلول في الرياضيات لمستوى الثانية بكالوريا علوم تجريبية مجمعة في كتاب واحد مفهرس لتصفح أي موضوع ا ضغط على عنوانه في الفهرس وللرجوع إلى الفهرس إضغط على تجميع وترتيب وفهرست ALMOHANNAD عضو بمنتديات دفاتر ملاحظات تعتبر الدالة Arctan خارج المقرر تعتبر المكاملة بتغيير المتغير خارج المقرر تعتبر المعادلات التفاضلية بطرف ثان خارج المقرر

الفهرس الموضوع 01 الحل الموضوع 02 الحل الموضوع 03 الحل الموضوع 04 الحل الموضوع 05 الحل الموضوع 06 الحل الموضوع 07 الحل الموضوع 08 الحل الموضوع 09 الحل الموضوع 10 الحل الموضوع 11 الحل الموضوع 12 الحل الموضوع 13 الحل الموضوع 14 الحل الموضوع 15 الحل
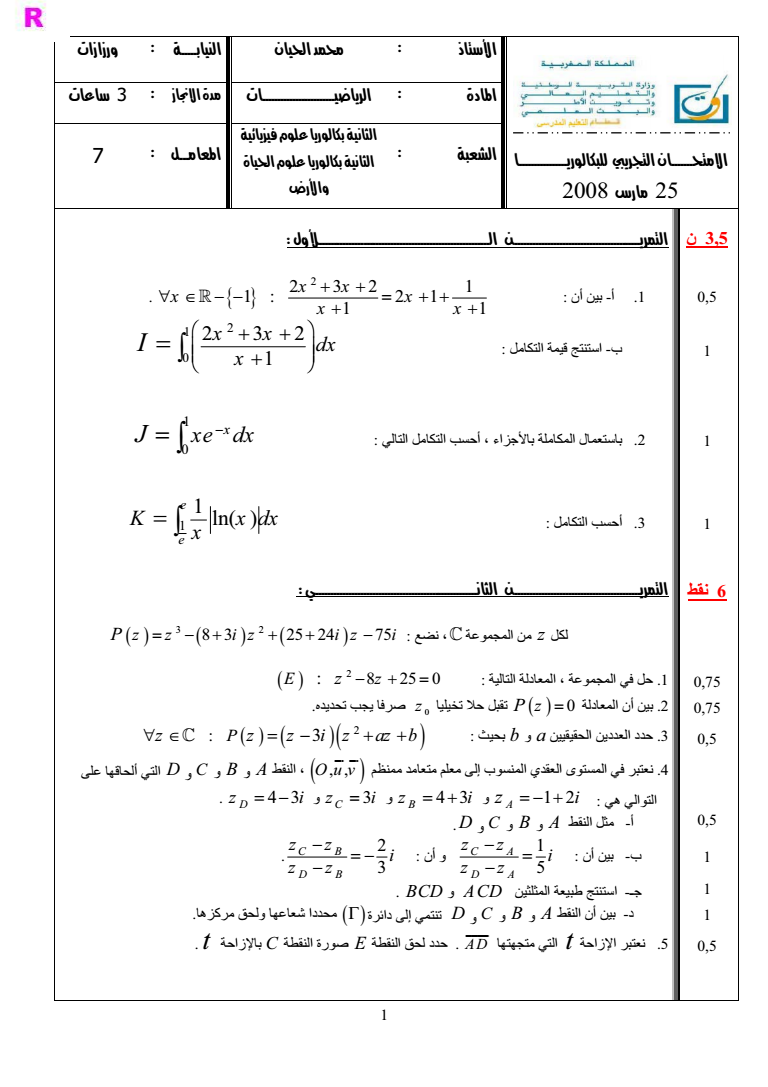
1 2008 25 quot amp 3 - 1quot 2 7 35 05 1 1 1 6 075 075 05 05 1 1 1 05 64quot53 - 1 2 2 32 1 1 2 1 1 1 x x x x x x - 2 1 2 32 1 x x dx x I 2 1 x J xe dx 1 3 1 ln e e K x dx x 67 03 amp quot z 3 2 P z z iz iz i 8 3 25 24 75 quot 1 2 E z z 8 25 0 6 9 P z 0 2 0 ltgt gt A z C b B a gt 3 2 z z z i z az b P 3 Ouv DE D F G quot H Iquot 9 amp 4 C B B B A J F K D B A 1 2 L quot 4 3 B z i B 3 B z i C z i D 4 3 B z i C B B B A J M - D B - 1 5 C A D A z z i z z B 2 3 C B D B z z i z z BCD B ACD MM 9O -N C B B B A J - PQ F G D B LR S B KT AD K K t UV 9 amp 5 t UV C W PXquotA E W S

2 105 05 1 15 1 05 1 1 05 1 075 075 1 68 03 gt F gt f 3 2 ln 1 0 4 3 0 fx x x fx xx x x B Cf Oi j DE D F G quot P Iquot f M F 0 W Z f - 1 Ramp 0 W T f - ln 1 lim 1 x t t R F Z 2 01 F gtgt B 1 B lim gtK - 3 x f x lim B x f x S - 3 3ln ln 1 0 fx x x x x x x F QKamp6 X -N Cf F abamp 4 Cf F f XquotZ h 5 9 h - 1 h ltgt D gt J F - 1 h x J x gt 9 amp 6 n n u gt 2 1 4 9 4 3 n nn n u u uu u n - 4 1 9 n un n - n u gtgt n -N n u K gtKamp De X

2BacSP amp 2BacSVT 2008 25 quot amp quot 2008 25amp - 0amp1 x 1 - 1 2 2 1 2 2 11 2 3 2 2 1 11 2 1 11 1 1 x x x xx x x x x x xx - 2 1 1 1 2 0 0 0 2 32 1 21 ln 1 2 1 1 ln 2 x x dx x dx x x x x x 2 11 1 1 00 0 0 x x xx J xe dx x e dx xe x e dx 1 1 1 1 11 0 0 1 2 1 x x J e e dx e e e e e ln x quot 3 1 e e ampquot 1 1 1 1 1 ln ln e e x dx x dx x x 1 1 1 1 11 1 ln ln ln e e e e x dx x dx x dx xx x K 1 1 1 ln ln ln ln e e x x dx x x dx 1 2 2 1 1 1 1 11 ln ln 0 0 2 2 1 2 2 e e Kx x 21 z amp 3 2 P z z iz iz i 8 3 25 24 75 ampquot 1 2 E z z 8 25 0 2 2 2 2 34 3 5 E 01 b ac i 4 1 25 16 25 9 3 1 4 3 b i z i a 2 4 3 6 b i z i a Si i 43 43 2 E 5 07 86 2 0 01 P z 0 4 lt 5 y 9quot z iy - 1 -

2BacSP amp 2BacSVT 2008 25 3 2 0 00 0 3 2 2 32 2 3 2 3 2 3 2 0 8 3 25 24 75 0 8 3 25 24 75 0 8 24 3 25 75 0 8 24 0 3 25 75 0 8 30 3 25 75 0 0 3 3 25 75 0 0 3 Pz z iz iz i iy i iy i iy i y yiy y y y y yy y y y yy y y y yy y Pz y 07 6 P z 0 gt4 lt amp5 2 z 0 3i 3 z i 3 3 amp3 P z 01 P z 6quot z 0 3i 1 b 25 6 a 8 0 A 86 quot amp 2 2 32 2 3 2 2 3 333 3 33 3 83 3 25 24 3 75 8 3 25 z z i z az b z z az bz iz aiz bi z z a i z b ai z bi ai i b ai i bi i a z z i z az b b P P P P Ouv 46 DE D P B3 C 4 Gquot D 6 C 6 B 6 A F3 4 1 2 2 A 4 3 6 z i B z i D 4 3 6 z i C 3 6 z i P B3 C D 6 C 6 B 6 A F3 ampH - - 2 -
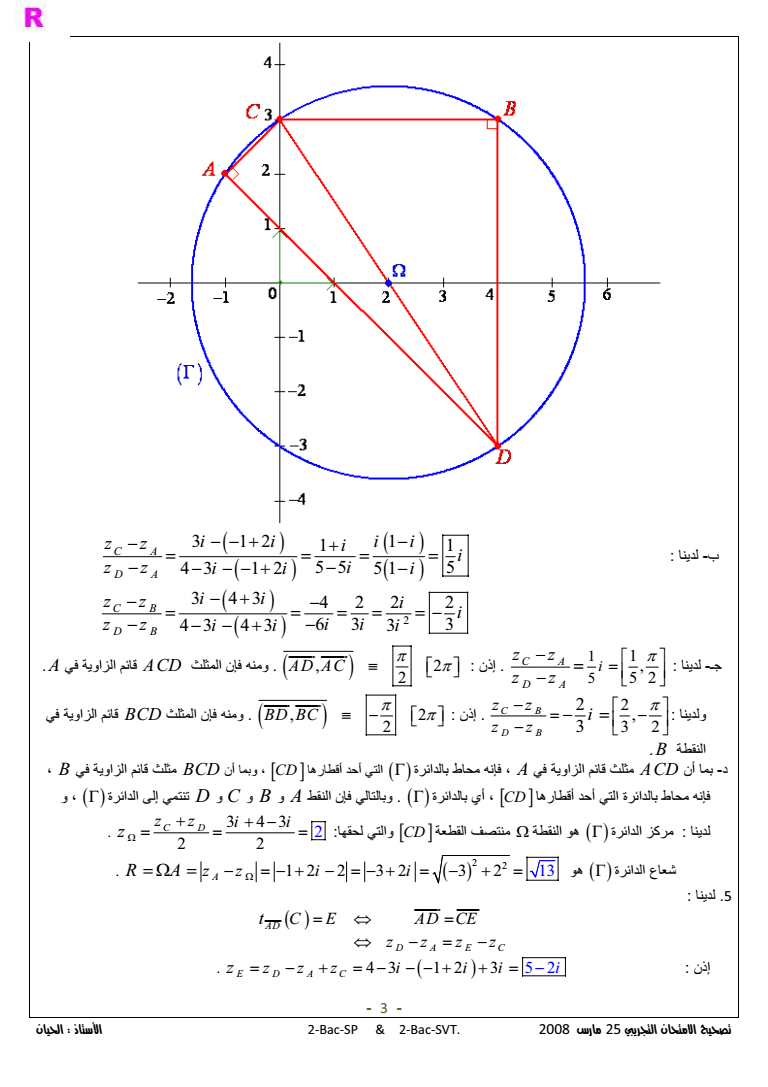
2BacSP amp 2BacSVT 2008 25 - 3 12 1 1 1 4 3 1 2 51 55 5 C A D A z z i i ii i i zz i ii i 2 3 43 422 2 43 43 63 3 3 C B D B z z i i i i zz ii i i i -I 1 5 1 5 2 C A D A i z z z z 2 01 2 AD AC A 6 DJ ACD 9H 07 86 6 2 3 2 2 3 C B D B z z z z i 2 01 2 BD BC 6 DJ BCD 9H 07 86 B K3 B 6 DJ 9H BCD 0 6 CD quot2K 5 4J Lquot 8 7 A 6 DJ 9H ACD 0 - 6 4J D 6 C 6 B 6 A F3 07 6 4J B CD quot2K 5 4J Lquot 8 7 G3quot 6 CD quotK3 N K3 2 4J M4 3 3 2 4 2 2 C D z z i i z 2 4J O 2 2 12 2 32 2 3 13 A R A zz i i 5 AD D E A C C E AD CE zzzz t 4 3 3 1 2 5 2 01 E D A C z zzz i i i i - 3 -

2BacSP amp 2BacSVT 2008 25 31 4 f 3 2 ln 1 0 4 3 0 fx x x fx xx x x 6 Cf Oi j DE D P C f ampH quot - 1 2 0 0 lim lim 43 0 x x fx xx x f amp amp 6 3 0 0 lim lim ln 1 ln1 0 0 x x f x xf amp amp 01 0 0 lim lim 0 x x fx fx f amp amp 0 K3 f 07 86 - 2 000 0 4 3 4 30 lim lim lim xxx fx f xx x x x x x ampampamp 0 0 6 0 P3Q f 01 d f 3 01 t x 0 0 x t amp 07 86 3 3 2 2 3 3 0 00 0 ln 1 ln 1 0 ln 1 lim lim lim lim 0 x xx t 0 x x fx f t x t xx t x amp ampamp amp 0 0 6 0 P3Q f 01 g f 0 00 0 6 g d f 0 0 6 0 K3 P3Q f 07 f f x 0 2 2 3 3 3 3 1 ln 1 1 3 0 1 x x x f x x x 2 6 3 0 x 3 1 0 x f 01 x 2 1 4 3 4 64 6 2 x xx x x x x x x x x x x f 2 4 6 1 1 6 6 6 1 x x x x x xx x x x f x f x 07 86 6 1x 2 1 f 01 01 - 3 2 lim lim lim 4 3 43 xx x fx xx x xx x amp amp amp 3 01 t x 1 x t amp 07 86 3 lim lim lim ln 1 ln xt t fx x t amp amp amp x 0 - 3 3 3 33 ln 1 ln ln 1 ln ln 1 ln 3 x x x x x x x xx x 3 3 3 ln 1 x x ln 1 x f x x x x - 4 -
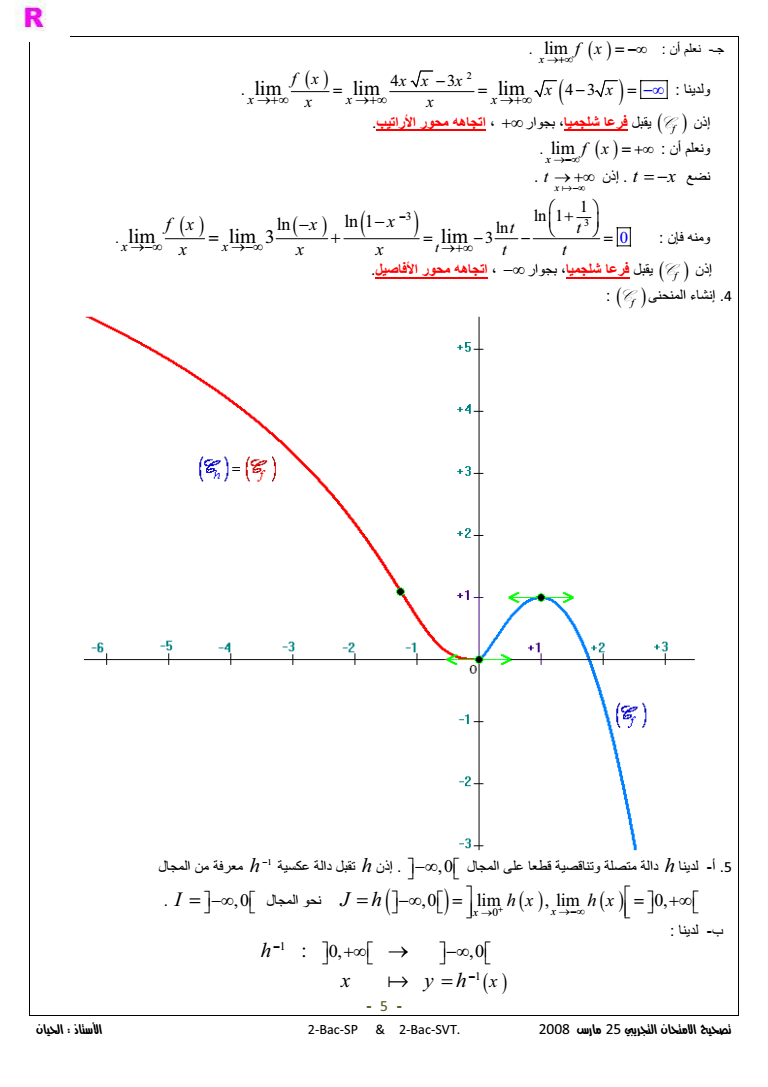
2BacSP amp 2BacSVT 2008 25 lim 0 D -I x f x amp 6 2 4 3 lim lim lim 4 3 xx x f x xx x x x amp amp amp x x 01 Cf 0 12- - amp3 lim 0 D 6 x f x amp 01 t x x t amp 07 86 3 3 1 n 0 ln 1 l 3 ln ln 1 lim lim lim 3 x x t t t t t fx x x x x x amp amp amp 01 Cf 34 12- - amp3 quot R 4 Cf K 6 h - 5 amp3 h 01 1 h 4 0 0 lim lim 0 x x J h hx hx amp amp I quot - 1 1 0 0 x h x yh amp - 5 -

2BacSP amp 2BacSVT 2008 25 x 9quot y 0 6 1 y h x V x S Tquot U 1 3 3 3 3 3 3 1 3 ln 1 1 1 1 1 1 0 1 x x x x x x y h x hy x y x y e y e y e y e ye y yhx y e 07 6 1 3 0 1 x x hx e 4 6 n n u M 4 2 1 4 9 43 n nn n n f u u u uu u n n 0 amp - 0 4 9 01 u 0 4 1 9 u 0 W4X n 4 1 9 un 1 4 1 9 n u f 4 1 9 0 1 1 4 48 1 9 81 4 4 1 11 9 9 n n n n u fff u u u 0 48 81 4 9 07 6 4 1 9 n un n - 2 1 n nn n n n n n 4 3 4 31 n u u uu u u u u u 3 3 1 31 1 u uuu u u u u n nn n n n n n 1 nn n n 1 31 n u uu u u 0 6 4 1 9 un 0 07 unn n 1 11 0 u u 6 un 6 2 1 23 3 13 12 3 uuu nnn 01 1 n uu 0 n n 07 86 n n u - 6 -

2BacSP amp 2BacSVT 2008 25 5 6 27 2 n 0 amp 4 9 1 0 6 u 4 48 9 81 u u f f 01 u u 1 0 u u n1 n 0 W4X n 6 u u n n 2 1 f 0 D 4 1 9 06 4 1 9 n u n 01 1 1 2 1 n n n n n n uu u u f f u u n u u n1 n 07 6 07 86 n n u 0 -I n n u 0 6 3 G 7 1 6 f 4 1 9 K 6 f 4 1 9 01 4 4 48 4 1 1 1 1 9 9 81 9 f f f 0 4 4 1 9 9 u n n u l GG 3 6 l l f 07 41 9 l 0 6 41 9 l lim 1 n 07 6 l 1 07 n u amp 38 n n u Archimde II plus Y 4 34 9 9 8 n n u 9 39 10 Maple 8 Y 4 - 7 -
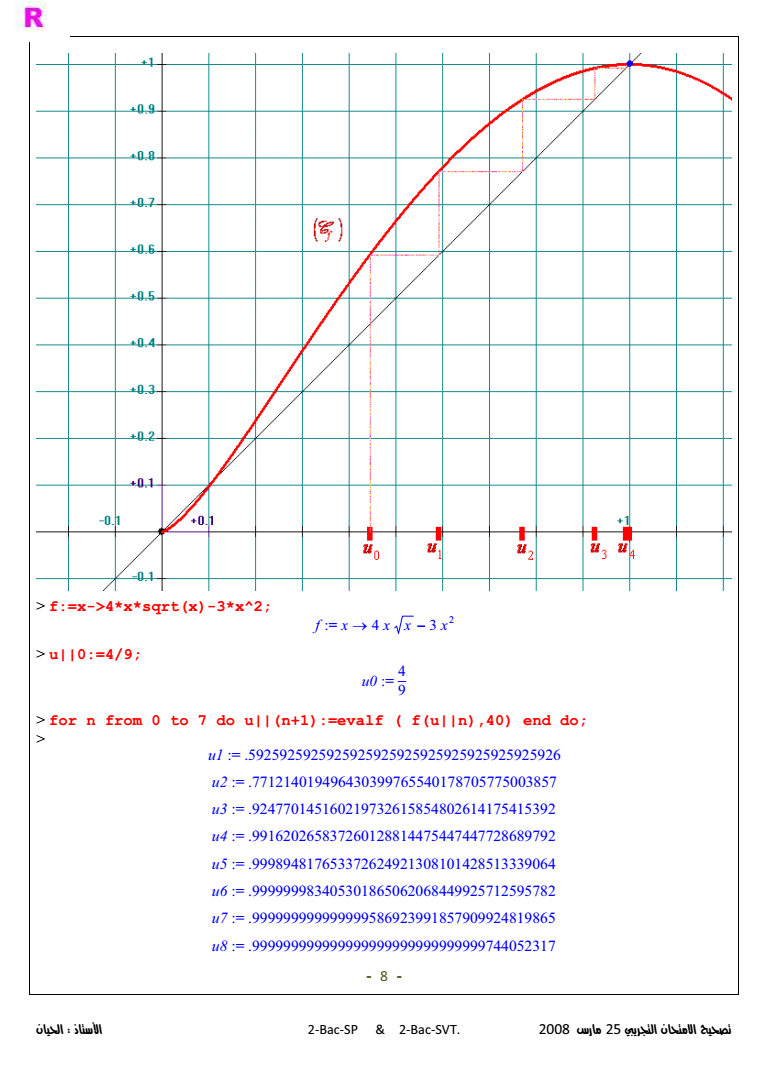
2BacSP amp 2BacSVT 2008 25 gt fx-gt4xsqrtx-3x2 gt u049 gt for n from 0 to 7 do un1evalf fun40 end do gt - 8 - f x-amp-4 x x --3 x2 u0 4 9 u1 5925925925925925925925925925925925925926 u2 771214019496430399765540178705775003857 u3 924770145160219732615854802614175415392 u4 991620265837260128814475447447728689792 u5 999894817653372624921308101428513339064 u6 999999983405301865062068449925712595782 u7 999999999999999586923991857909924819865 u8 999999999999999999999999999999744052317

ثانوية بئر أنزر رو الانية بكالوريا علوم فيزيائية 2 2008 - 2007 yjvmbzna 2008b e1 2d الشعبة علوم تجريبية المدة 3 ات توفيق بنعمر يسمح باستعمال الآلة الحاسبة غير القابلة للبرمجة G G التمرين 1 المستوى العقدي منسوب لمعلم متعام ممنظم O uv 075 05 05 025 05 05 0 في ل 1 2 z z 2 2 z i C B A أكتب لحين على ال كل المثلثي 1 والي على ألحاقها التي القط نعتبر 2 B A A z z C B 2 z z 3 حدد كل الجبري المثلثي ل 3 c A z z IAC I3 I C E JJJG 2 4 Ez i E D لتكن لنقطة استنتج طبيعة المثلث حيث 3 لتكن النقطة صورة O بالإزاحة 2 تحقق 4 حدد لحق النقطة صورة با ور مسألة 05 025 075 05 1 075 125 05 1 05 075 1 x f x e الجزء الأول عتبر الدالة f المع فة على بما يلي 1 ln1 lim 1 x f x lim x f x 1 ln1 x D y x x f x x f D 1 بين عط للنتيجة بين 2 تحق e استنتج 1 مقارب مائل ار حدد ضع النسبي ل C نبي 3 1 1 x x f x e f a a e ln 1 f f 0 03 f 1 f 1 J f ضع جدول التغيرات 4 أحسب f a عط لهما a 06 2cm الوحدة معلم في C أنشئ 5 6 بين تقبل دال سية مع فة على مجال تحديده أنشئ في نفس المعلم المنحنى C n n u 0 لجزء الثاني نعتبر المتتالية المع فة بما يلي 1 2 n n 1 u u 0 n n u x f x x x n n u n n u u f 1 بين بالترجع a nbi a نبي 2 بين المتتال تزايدية 3 استنتج متقاربة حدد نهايتها 2 R O

ثانوية ئر نزران صفرو موضوع امتحان تجريبي - 2008 2007 - مادة ال ياضيات 2 بك لوريا لوم يزيائية 2 e 2 2 d 2 التمرين O i j k ممنظم متعامد لمعلم منسوب الفضاء G G G R x y z 2 0 P x z 1 0 نعتبر 05 075 05 025 1 1 بين R P متعامدان R P n 1 21 S تحقق مو هة للمستقيم تقاط حدد تمثيل بارمتري له G 2 11 نعتبر التي مركزها O المماسة بين شعاعاها هو 6 S S P حدد معادلة ديكارتية ل بين وفق دائرة مركزها شعاعها E y quot 4y 13y 0 المعادلة نعتبر 3 التمرين 05 05 075 1 1 ل المعادلة لتفا E 0 E g g 0 3 g0 يحقق الذي ل دحد 2 استنتج سب باستعمال مكاملة بالأجزاء ل dx التمرين 4 السؤالان 2 1 مستقلان فيما بينهم 075 05 1 نعتبر مكعب وجهه مرمة من 1 إلى 6 نرمي ذا الرد مرة حدة نسجل ال قم الم ل عليه نعتبر الحدثين A quot الرقم المحصل ليه أصغر أو يساوي B quot 4 quot الرقم الم ل عليه فردي quot B p A p A أحسب نرمي هذ الرد 5 مرات أحسب احتمال لحصول على عدد فردي مرتين بال بط 125 U 2 صندوق يحتوي على كرتين خضراوين ثلاث كرات صفراء U صندوق يحتوي على ثلاث كرات خضراء كرة واحدة بيضاء X X نسحب تآني عشوائي كرتين من U نسحب عشوائي بالتتابع دون حلال كرتين من U فنحصل على أربع كرات ليكن المتغير العشوائي المرتبط بعدد الألوان المحصل عليها حدد قانون احتمال المتغير العشوائي 2 2 3 sin3 1 13 x e x dx e 2 cos3 x I e x nbi

ثانوية بئر أنزران صفرو الانية بكالوريا علوم فيزيائية 2 2008 - 2007 ypabg 2008bjvnabzna e1 4d الشعبة علوم تجريبية المدة 3 اعات توفيق بنعمر التمرين الأول 1 المميز 4 إذن d i 2 جذر مربع له منه لحلان هما 2 2 2 1 2 i z i 2 1 2 2 1 2 i z i 1z i 1 2 4 2 4 z 2 2 2 3 1 2 1 2 2 5 1 5 5 z i i i i i 3 2 C z i حسب ما سبق A لدينا 3 1 3 C A z z منه 3 3 إذن C A CI AI z z JJG JJG z 3 lt arg 2 لدينا 3 2 C A IA IC z C 2 22 2 3 2 4 E O C I E z z z z z i إذن IA متساوي الساقين قائم ال اوية في I t O JJG E 2IC OE JJG JJJG 3 1 1 0 1 1 1 x x x x x x x e e e f x e e e e e x f x gt x 1 x 3 i 0 لدينا 2IC x 0 x e gt 4 2 2 2 4 4 2 i D O E O o D R E D z z e z z z i i i z z D O 4 مسألة الجزء الأول ذن lim 0 1 x x e lim 1 ln1 0 1 x f x y 1 x إذن المستقيم ذو المعادلة مقارب أفقي بجوار a lim x x e lim ln1 ذن x e lim lim 1 ln1 x x x f x e 1 ln1 1 ln 1 1 ln ln 1 1 ln 1 1 ln 1 x x x x x x x f x e e e e e x e x e m 0 x e lim 1 lim ln 1 ln1 0 x f x x e 1 ln 1 x f x y f x x e 0 1 1 ln 1 ln1 ln 1 0 ln 1 0 x x x x x x e e e e e f x y gt gt gt gt lt f ذن لدينا li إذن nbi ذن C يوجد حت على 1 f x f x ln 1 1 ln1 1 ln1 1 ln1 1 1 ln 1 1 0 a e f a e e e e ذن يقطع محور الأفاصيل في النقطة Cf A a 0 ln 1 1 ln1 1 ln1 1 1 1 1 ln1 1 ln 1 1 1 ln 1 ln ln 1 ln 1 1 a e f a e e e e e e e e e e f B a a الن في y x يقطع C ذن 1
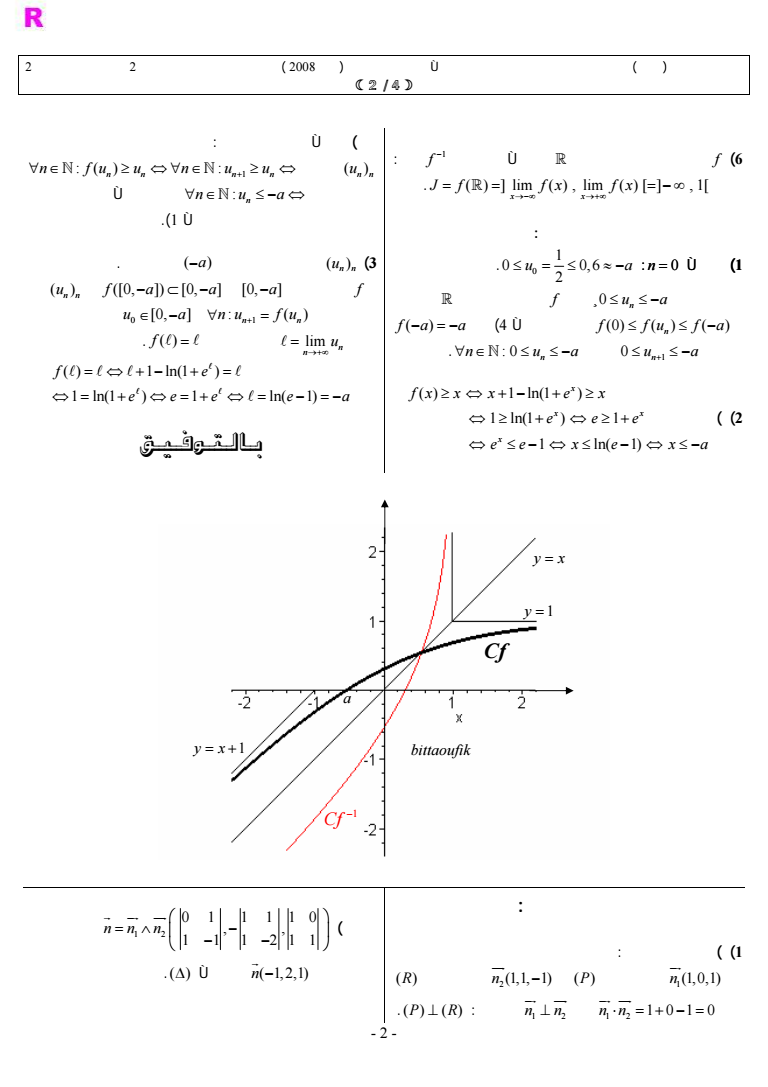
ثانوية ئر نزران صفرو إشارات حلول الا تحان التجريبي ماي 2 2008 بك لوريا لوم يزيائية 2 e 2 4 d f 6 متصلة تزايدية على ذن تقبل دالة كسية على lim lim 1 x x J f f x f x 1 f n n تزايدية u الجزء الثاني n 0 أجل من 1 0 1 0 06 2 u a 0 n f u a 0 n f a f f u f n u 0 1 ln1 1 1 ln 1 x x x e e e e e x e x 1 n n n n n f u u n u u n n u a n n a u f a 0 0 f n n u n n f u 0 u a 0 lim n n u f A A A 1 ln1 1 ln1 1 ln 1 f e e e e e A A A A A A A A لدينا تزايدية لى ذن a سب ال ال a 4 إذن 1 0 n u a a منه n 1 ln1 x a f x x x e x 2 a نستعمل التكافؤات المتوالية حسب ال السابق هذا صحيح سب السؤال 1 3 تزايدية مكبورة ذن بة a 0a على متصلة متقاربة 1 n u ذن يحقق ال nbi التمرين الثاني المعادلتين من لدينا 1 JG منظمية n 1 101 2 n 111 JJG R 1 2 1 0 1 JJG 1 2 n n JJG P R P على n n 0 JG إذن JG بالتالي G JG JJ 1 2 0 1 1 1 1 0 1 1 1 2 1 1 n n n G n 1 21 G ل هة مو ذن y x y x 1 Cf y 1 a bittaoufik 1 Cf - 2 -

ثانوية ئر نزران صفرو إشارات حلول الا تحان التجريبي ماي 2 2008 بك لوريا لوم يزيائية 2 e 3 4 d نحدد نقطة مشتركة R P x 1 z 0 0 y z 2 3 x R 1 3 2 x t y t t z t نأخذ ذن في مع لة P نع ضهما في R ذن ذن منه A 1 3 مشتركة P لدينا إذن تنتمي ل لدينا 0 بالتالي تمثيل منه إذن 2 شعاع الفلكة هو مسافة المركز O عن OA n R d O n JJJG G G 11 11 6 6 R 2 2 2 11 6 x y z إذن OA OA n دنحد JJJG G n 311 فنجد JJJG G nbi نحدد مسافة O عن P شعاع الدائرة 0 0 1 1 1 0 1 2 d d O P lt R نحدد المركز المستقيم المار من O العمودي 2 2 4 2 3 3 3 r R d 1 JG P D x t D y t z t 1 2 e 1 إذن n مو هة له منه تمثيله 2 نع ضه في P فنجد t إذن نقطة القاطع لدائرة مركز هي 1 1 0 2 2 c التمرين الثالث زالممي 0 المم المعادلة 1 2 36 r r 4 13 r i 2 3 d i 6 2 cos3 sin3 x y x e x x 2 cos3 sin3 x g x e x x 0 cos0 sin 0 0 2 sin2 x g x e x 2 2 2 sin3 3cos3 x x g x e x e x 0 3 2 sin3 x g x e x g x 4g x 13gx 4 2 6 3 p A 2 1 6 3 p A B 3 1 6 2 p B جذر مربع الحلان حلول المعادلة التفاضلية تب على شكل 2 منه إذن g0 0 بالتالي 1 إذن g 4 1 13 13 g x g x g x 2 0 0 0 0 0 0 2 2 sin3 4 1 13 13 4 1 13 13 4 1 0 0 13 13 1 3 0 3 3 1 13 13 x e x dx g x dx g x dx g x dx g x g x g g g g e e os3x 2 x e 3sin3x مكاملة بالأجزاء إذن v x u x c ضع u x منه 1 2 2 x v x e 2 2 2 0 0 2 2 cos3 1 3 cos3 sin3 2 2 1 1 3 3 2 1 2 2 2 13 13 x x x I e x dx e x e x dx e e التمرين الرابع ltlt 5 - 3 - 1 gtgt B ltlt 4 - 3 - 2 - 1 gtgt A 1 إذن ltlt 3 - 1 gtgt A B بالتالي 3 B p A B p A p B n 5 2 الاختبار عاد خمس مرات باستقلالية B دث 1 2 p p B 3

ثانوية ئر نزران صفرو إشارات حلول الا تحان التجريبي ماي 2 2008 بك لوريا لوم يزيائية 2 e 4 4 d احتمال أن يتحقق B مرتين k 2 هو 2 2 3 5 1 1 1 2 2 C 2 3 U V J 3 1 U V B 2 2 4 5 card A C 1210 120 5 16 2 عدد الألوا المسحوبة هو لون أو لونان أو ثلاث ألوان nbi نسحب تآني كرتين ذن نستعمل عدد التأليفات نسحب بتتابع ون إحلال ذن نستعمل عدد الرتيبات عدد الإمكانيات 3 2 2 2 6 1 1 120 120 20 A C p X U X 1 2 U V 2V 1 1 2 2 2 2 1 1 1 3 2 3 3 3 3 2 2 60 1 2 120 120 2 A A C A C A C C p X V J 1 2 U V 2 U V 1 U B V X 2 1 U 2 U J 2 U V 1 1 1 2 1 111 1 3 3 1 3 3 2 2 2 54 9 3 120 120 20 A A C A A C C p X 1 1 U B V 1 U B V X 3 1 1 U V J 2 U J 1 4

1 الامتحان التجريبي المملكة المغربية وزارة التربية الوطنية والتعليم العالي و تكوين الأطر و البحث العلمي الأآاديمية الجهوية للتربية والتكوين جهة الشاوية ورديغة-سطات نيابة خريبكة ثانوية يوسف بن تاشفين التأهيلية أبريل 2007 المادة الرياضيات المستوى 2سلك الباآالوريا الشعبة علوم تجريبية المعامل 7 المدة 3ساعات تمرين1 G G G الفضاء منسوب لمعلم متعامد و ممنظم ومباشر Oi jk C 1 0 1 B 1 4 0 A 0 1 1 النقط نعتبر AB AC المتجهي الجداء أحسب أ 1 JJJG JJJG ب استنتج معادلة ديكارتية للمستوى ABC 2 لتكن S مجموعة النقط M xyz من الفضاء حيث 222 13 226 0 2 xyz xyz 2 أ بين أن S فلكة شعاعها 3 2 احداثياتمرآزها محددا R ب بين أن المستوى ABC مماس للفلكة S تمرين2 المتتالية العددية المعرفة ب n n u نعتبر 1 3 2 1 1 n n u u un n u 1 2 n أن بين -1 متقاربة n n u تزايدية و استنتج أن 2 n u- بين أن n n نعتبر -3 n v ln 1 ب المعرفة المتتالية n n nv u 1 متتالية هندسية أساسها n n v أ- بين أن 2 الأول حدها و 0 v ln 2 lim n حدد -ب n v lim استنتج و n n u تمرين3 أن تأآد -1 2 2 1 3 4 i i المعادلة في نعتبر -2 3 2 E z z iz i 2 4 1 161 0 أ تأآد أن 4حل للمعادلة E ب حدد العددين b و a حيث 32 2 z z i z i z z az b 2 4 1 161 4 ج حدد z1 و z2 جدري المعادلة 2 z zz i 2 41 0 د استنتج حلول المعادلة E 3- أآتب حلول المعادلة E في شكلها المثلثي 4 1 2 Oe e- في المستوى العقدي المنسوب إلى المعلم المتعامد الممنظم G G نعتبر النقط A و B و C التي ألحاقها4 و 2i و 2 2 i على التوالي بين أن ABC مثلث قائم الزاوية و متساوي الساقين في B 0200 050 050 050 050 0300 050 075 075 100 0400 025 025 075 075 025 075 100

2 الامتحان التجريبي أبريل2007 تمرين4 يحتوي صندوق على 7 بيادق سوداء مرقمة أربعة بيادق منها تحمل الرقم 1 و البيادق الاخرى تحمل رقم 2 و ثلاث بيادق بيضاء بيدقان منها تحمل الرقم 1 و البيدق الاخر يحمل الرقم 2 نسحب بالتتابع و بدون إحلال بيدقين 1- أحسب احتمال الحصول على بيدقين مجموع رقميهما زوجي 2- أحسب احتمال الحصول على بيدقين سوداوين علما أن مجموع رقميهما زوجي تمرين5 ب 0 على المعرفة العددية الدالة g لتكن A 1 ln 1 ln 1 1 gx x x x lim 1 أن بين -1 x g x 2- بين أن 2 1 1 g x x x لكل x من 0 و استنتج منحى تغيرات g على 0 x gx 0 0 أن استنتج -3 B لتكن f الدالة العددية للمتغير الحقيقي المعرفة على ب 1 ln 1 0 1 0 x x fx x x x x f x xe x و للدالة الممثل المنحنى Cf Oi j ممنظم متعامد معلم في f G G i j cm 2 حيث G G أن بين أ -1 1 lim ln 1 x x x x lim استنتج ثم x f x lim حدد ب x f x و أول النتيجة هندسيا ج بين أن f متصلة في 0 2- أدرس قابلية اشتقاق f على اليمين في 0 و على اليسار في 0 ثم أول النتيجتين هندسيا 0 أن و x 0 f x gx أن بين أ -3 x x f x xe ب أعط جدول تغيرات f 4 Cf- بين أن النقطة A ذات الافصول 1- نقطة انعطاف للمنحنى بجوار 5 Cf- بين أن المستقيم ذا المعادلة y x 2 مقارب للمنحنى 6 Cf- أنشئ المنحنى ln 3 11 ln 2 07 1 e 037 2 e 014 3 e 005 0200 1 1 0900 050 075 050 075 075 075 125 125 050 050 050 100

httparabmathsiftfr 1 الامتحان التجريبي المملكة المغربية وزارة التربية الوطنية والتعليم العالي و تكوين الأطر و البحث العلمي الأآاديمية الجهوية للتربية والتكوين جهة الشاوية ورديغة-سطات نيابة خريبكة ثانوية يوسف بن تاشفين التأهيلية أبريل 2007 المادة الرياضيات المستوى 2سلك الباآالوريا الشعبة علوم تجريبية المعامل 7 المدة 3ساعات تمرين1 AB AC نحسب أ 1 JJJG JJJG AB13 1 منه و C 1 0 1 B 1 4 0 A 0 1 1 لدينا JJJG AC 1-10 و JJJG 1 1 1 0 1 1 3 4 1 1 1 Z Y X AB AC 1 1 4 JJJG JJJG ب نستنتج معادلة ديكارتية للمستوى ABC AB AC 1 1 4 JJJG JJJG ABC -x-y-4zd0 منه و ABC المستوى على منظمية ABC -x-y-4z50 إذن d 5 فان A 0 1 1 ABC أن حيث و - 2 2 أ نبين أن S فلكة شعاعها 3 2 احداثياتمرآزها تحديد مع R 222 222 13 2 2 6 0 2 9 1 1 3 2 M xyz S x y z x y z M xyz S x y z 2 إذن S فلكة شعاعها 3 2 113 ومرآزها R ب نبين أن المستوى ABC مماس للفلكة S S الفلكة مرآز 113 و ABC -x-y-4z50 لدينا 1 1 12 5 9 32 1 1 16 18 2 d ABC R إذن المستوى ABC مماس للفلكة S تمرين2 المتتالية العددية المعرفة ب n n u 1 3 2 1 1 n n u u un n u 1 2 n أن نبين -1 0 من أجل n 0 لدينا 3 2 1 2 u0 ومنه u 1 2 أن نفترض n أن نبين n الرتبة حتى صحيحة عبارة u 1 1 2 n u 1 2 لدينا n 0 11 منه و u n u 0 11 بالتالي و n 1 2 un1 أن أي 11 1 2 un منه و u 1 2 إذن n u n

httparabmathsiftfr 2 متقاربة n n u تزايدية و نستنتج أن 2 n u- نبين أن n ليكن n 1 1 1 11 1 nn n n n n uu u u u u 1 2 أن بما n 01 1 فان u n u ومنه 1 0 n n u u n إذن n u تزايدية متقاربة n u مكبورة بالعدد 2 فان n n u n و حيث أن n نعتبر -3 n v ln 1 ب المعرفة المتتالية n n nv u 1 متتالية هندسية أساسها n n v أ- نبين أن 2 الأول حدها و 0v ln 2 ليكن n 1 1 1 1 ln 1 ln 1 ln 1 2 2 nn n n n vu u u v n n v أساسها هندسية متتالية 1 0 0 و حدها الأول 2 3 ln 1 ln 1 ln 2 2 v u lim n نحدد -ب n v lim نستنتج و n n u 1 متتالية هندسية أساسها n n v لدينا 2 الأول حدها و 0 v ln 2 و منه 1 ln 2 2 n n v 1 lim lim ln 2 0 2 n n n n v ln 1 لدينا n n 1 n ومنه nv u v n n eu lim lim 1 2 اذن n v n n n u e تمرين3 أن نتأآد -1 2 2 1 3 4 i i 2 2 1 4 4 1 3 4 i ii المعادلة في نعتبر -2 3 2 E z z iz i 2 4 1 161 0 أ نتأآد أن 4حل للمعادلة E 3 2 4 2 4 4 1 4 161 64 32 16 16 16 16 0 i i ii اذن 4حل للمعادلة E ب نحدد العددين b و a حيث 32 2 z z i z i z z az b 2 4 1 161 4 2 32 z z z az b z a z a b z b 4 4 4 4 وحيث 32 2 z z z i z i z z az b 2 4 1 161 4 4 2 4 16 1 4 4 1 a b i ab i منه و a bi 2 41 اذن ج نحدد z1 و z2 جدري المعادلة 2 z zz i 2 41 0 للمعادلة المختصر الميز ليكن 2 2 1 41 3 4 2 1 i ii منه و 1 zi i 2 1 2 1 22 و z ii 1 21 2

httparabmathsiftfr 3 د نستنتج حلول المعادلة E لدينا 32 2 z z z iz i z z z i 2 4 1 161 4 2 4 1 2 4 2 4 1 0 4 2 22 E z zz i E z ou z i ou z i اذن حلول المعادلة E هي 4 و 2i و 2 2 i 3- نكتب حلول المعادلة E في شكلها المثلثي 2 2 و 4 4 2 i و 2 2 2 2 2 2 2 2 22 4 i i 4 1 2 Oe e- المستوى العقدي المنسوب إلى المعلم المتعامد الممنظم G G نبين أن ABC مثلث قائم الزاوية و متساوي الساقين في B لديناA و B و C النقط التي ألحاقها 4 و 2i و 2 2 i على التوالي n n n n n 22 2 arg 2 4 2 2 4 arg 2 4 2 2 4 arg 2 4 2 arg 2 2 2 i i BA BC i i BA BC i i i BA BC i BA BC i BA BC JJJG JJJG JJJG JJJG JJJG JJJG JJJG JJJG JJJG JJJG nABC اذن قائمة زاوية BA BC منه و BA i BC i 4 2 20 2 4 20 لدينا اذن ABC مثلث قائم الزاوية و متساوي الساقين في B تمرين4 الصندوق يحتوي على 7 بيادق سوداء مرقمة أربعة بيادق منها تحمل الرقم 1 و البيادق الاخرى تحمل رقم 2 و ثلاث بيادق بيضاء بيدقان منها تحمل الرقم 1 و البيدق الاخر يحمل الرقم 2 نسحب بالتتابع و بدون إحلال بيدقين 1- نحسب احتمال الحصول على بيدقين مجموع رقميهما زوجي نعتبر الحدث A quotالحصول على بيدقين مجموع رقميهما زوجيquot 2 2 6 4 2 10 65 43 7 10 9 15 A A P A A 3- نحسب احتمال الحصول على بيدقين سوداوين علما أن مجموع رقميهما زوجي نعتبر الحدث N quotالحصول على بيدقين سوداوينquot 2 2 3 4 2 10 15 3 2 4 3 15 1 3 7 7 10 9 7 5 7 15 A A A PA N A P N P A تمرين5

httparabmathsiftfr 4 ب 0 على المعرفة العددية الدالة g A 1 ln 1 ln 1 1 gx x x x lim 1 أن نبين -1 x g x 1 11 lim lim ln 1 ln 1 lim ln1 1 1 xx x 1 1 gx x x x xx 2- نبين أن 2 1 1 g x x x لكل x من 0 و نستنتج منحى تغيرات g على 0 0 من x ليكن 1 ln 1 ln 1 1 gx x x x و منه 2 2 2 22 2 2 1 1 1 21 1 1 1 1 11 1 1 xx x x x xx x x g x x x x xx xx xx 2 1 0 0 1 x x x x gx 0 0 أي اذن g تناقصية قطعا على 0 x gx 0 0 أن نستنتج -3 x لدينا g تناقصية قطعا على 0 و lim 1 g x x gx 0 0 اذن f B الدالة العددية للمتغير الحقيقي المعرفة على ب 1 ln 1 0 1 0 x x fx x x x x f x xe x أن نبين أ -1 1 lim ln 1 x x x x lim نستنتج ثم x f x 1 نضع x t 1 ومنه t و بالتالي x 1 ln 1 lim ln lim 1 x t x t x x t منه و 1 lim lim ln 1 x x x fx x x x lim نحدد ب x f x ونؤول النتيجة هندسيا lim lim 1 lim 0 x xx xx x f x x e e xe Cf و منه محور الافاصيل مقارب للمنحنى ج نبين أن f متصلة في 0 00 0 1 lim lim ln 1 lim ln 1 ln 1 1 xx x x fx x x x x x x x x 0 0 lim lim 1 1 x x x f x xe ومنه 0 0 lim lim 0 x x fx fx f اذن f متصلة في 0 2- ندرس قابلية اشتقاق f على اليمين في 0 و على اليسار في 0 ثم نؤول النتيجتين هندسيا

httparabmathsiftfr 5 0 00 0 11 1 lim lim lim 1 1 0 x x x x xx f x f xe e e x xx و منه f قابلية اشتقاق على اليسار في 0 و تقبل نصف مماس أفقي على يسار في 0 00 0 1 ln 0 1 lim lim lim ln 1 1 xx x x x x fx f x xx x و منه f غير قابلية الاشتقاق على اليمين في 0 و تقبل نصف مماس عمودي على يمين في 0 0 أن و x 0 f x gx أن نبين أ -3 x x f x xe x 0 ليكن 1 ln 1 x f xx x x 2 1 1 1 ln 1 ln 1 ln 1 1 1 x x f x x x x gx x x x x 1 x 0 ليكن x f x xe 1 x xx f x e x e xe ب نعطي جدول تغيرات f x 0 f x f x 4 Cf- نبين أن النقطة A ذات الافصول 1- نقطة انعطاف للمنحنى x 0 ليكن x f x xe 1 x x x f x e xe x e 1 0 1 x fx x e x x -1 0 f x 0 - Cf اذن النقطة A ذات الافصول 1- نقطة انعطاف للمنحنى بجوار 5 Cf- نبين أن المستقيم ذا المعادلة y x 2 مقارب للمنحنى 1 lim 2 lim ln 1 1 1 0 x x x fx x x x بجوار Cf اذن المستقيم ذا المعادلة y x 2 مقارب للمنحنى 6 Cf- ننشئ المنحنى
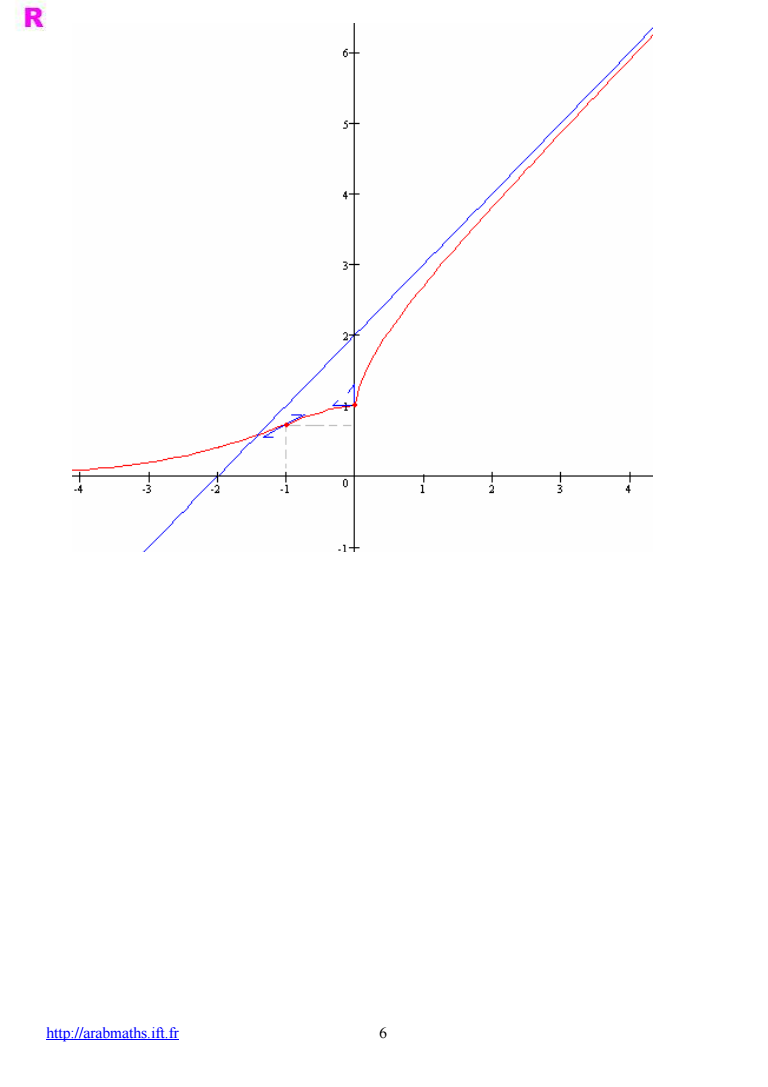
httparabmathsiftfr 6
المستوى الثانية باآلوريا الشعبة علوم تجريبية الامتحان التجريبي الموحد مدة الإنجاز ثلاث ساعات ثانوية موسى بن نصير سيدي يوسف بن علي 2006 2005 مراآش 1 2 سلم التنقيط 05 025 05 05 025 05 05 التمرين الأول 3 ن في الفضاء المنسوب إلى معلم متعامد ممنظم مباشر نعتبر النقط 011 و 110و 0 1 1 C JJJG JJJJG C احسب - a 1 b- استنتج أن النقط و و C غير مستقيمية 2 تحقق أن معادلة ديكارتية للمستوى C هي xyz 0 2 22 xyz x y 2 4 40 3 لتكن الفلكة S التي معادلتها هي a- حدد مرآز و شعاع S b- بين أن المستوى C يقطع الفلكة S وفق دائرة c- حدد مرآز وشعاع 4 حدد معادلة ديكارتية لكل من المستويين الموازيين للمستوى C و المماسين للفلكة S 025 05 05 05 05 05 025 05 التمرين الثاني 35 ن المعادلة نعتبر 2 E z z iz i 33 22 3 0 a 1- حدد الشكل الجبري للعدد العقدي 2 3 i b - حل المعادلة E نعتبر النقط وو C التي ألحاقها هي 2 JG JG في المستوى العقدي P المنسوب إلى معلم متعامد ممنظم R Oi j التوالي على c i 3 3 و b i 3 و a i 2 a اآتب b و c على الشكل المثلثي b أنشئ النقط و و C العدد اآتب -a 3 b a c a C على الشكل المثلثي b- استنتج طبيعة المثلث bca a 4 - تحقق أن O C الرباعي طبيعة استنتج -b 05 05 05 التمرين الثالث 15 ن صندوق 3 يضم آرات تحمل الرقم 0 و آرتين تحملان الرقم 1 وصندوق يضم آرتين تحملان الرقم 0 و آرتين تحملان الرقم 1 نسحب بالتتابع وبدون إحلال آرتين من ثم نسحب آرة واحدة من 1 ما هو عدد النتائج الممكنة 2 ما هو عدد النتائج التي تكون فيها الكرات الثلات تحمل الرقم 0 3 ما هو عدد النتائج التي يكون فيها مجموع أرقام الكرات الثلاث يساوي 2 1 025 025 05 التمرين الرابع 2 ن 1 احسب التكاملين 1 1 x و e dx 1 2 1 ln e dx e x x ليكن 2 4 3 x a تحقق أن 2 2 2 1 1 tan sin tan x x x احسب b 3 2 4 1 sin dx x سب التكامل cos ln 1 e 3 باستعمال المكاملة بالأجزاء مرتين اح J x dx

المستوى الثانية باآلوريا الشعبة علوم تجريبية الامتحان التجريبي الموحد مدة الإنجاز ثلاث ساعات ثانوية موسى بن نصير سيدي يوسف بن علي 2006 2005 مراآش 2 2 سلم التنقيط 05 025 025 05 075 075 125 025 05 05 025 05 1 05 05 05 05 075 مسألة 10 ن الجزء الأول x gx e x نعتبر الدالة العددية g المعرفة على آما يلي 1 lim g x x g x g x و lim احسب 1 x x لكل احسب - a 2 g b- ضع جدول تغيرات الدالة أنه استنتج -c x gx gt 0 3 بين أن للمعادلة x gx x حلا وحيدا في المجال 12 الجزء الثاني 1 لتكن الدالة العددية f للمتغير الحقيقي x بحيث ln 1 0 1 1 0 x x fx e x x fx e x x lt P f R Oi j وليكن C المنحنى الممثل للدالة f في المستوى المنسوب إلى معلم متعام د ممنظم JG JG f عند و Df ونهايتي 1 حدد 2 بين أن 0 limx x fx f x gt 0 و 0 lim 0 x x fx f x lt ثم أعط تأويلا جبريا و هندسيا للنتيجة أنه بين -a 3 0 1 x e gx x fx x b - احسب f x لكل x 0 و بين أن إشارتها هي إشارة 1 x على هذا المجال c- ضع جدول التغيرات للدالة f أن بين - a 4 lim 0 x f x x b- ادرس الفروع اللانهائية للمنحنى Cf c Cf- أنشئ المنحنى 5 f احسب مساحة الحيز المحصور بين المنحنى C و محور الأفاصيل و المستقيمان اللذان معادلتهما هي x 0 و x 1 الجزء الثالث U n لتكن المتتالية العددية المعرفة بما يلي 1 ln2 n n U n U gU هو العدد الوارد في السؤال الثالث من الجزء 1 ن 0 lt lt lt الأول 1 احسب U و تحقق أ U U 1 0 0 أنه بين 2 n U ltlt n U n U n 3 بين أن تناقصية 4 استنتج أن متقاربة و احسب نهايتها ملاحظة يراعى في التصحيح سلامة التعبير و حسن التقديم حظ سعيد للجميع

تصحيح الامتحان التجريبي الموحد 2006 ثانوية موسى بن نصير مراآش سيدي يوسف بن علي إعداد ذ موماد التمرين الأول AB 10 1 لدينا - a 1 JJJG AC 0 2 2 و JJJJG إذن 0 2 1 0 10 12 12 02 222 2 AB AC i j i j k i jk k JJJG JJJJG JG JG JG JG JG JG JG JG JG النقط فإن AB AC 0 أن بما -b JJJG JJJJG G مستقيمية غير C و B و A ni jk المتجهة أن a 1 من نستنتج 2 JG JG JG JG على منظمية المستوى ABC إذن معادلة هذا الأخير هي على شكل x y z d 0 فإن بالتالي و d 0 فإن A 011 ABC أن وبما ABC x y z 0 a 3 - يمكن لمعادلة الفلكة S أن تكتب 2 22 1 2 1 xy z 2 R 1 هو S شعاع إذن 1 20 هو مرآزها و b - لتكن d مسافة عن المستوى ABC لدينا 2 2 120 1 3 1 1 1 3 3 2 بالتالي و d R lt إذن d فإن المستوى ABC يقطع الفلكة S وفق دائرة شعاعR ليكن - c 2 2 6 3 R Rd ز نجد من Hx y z H HH لتكن النقطة مرآ 0 H z H H x y 1 و 2 H H H x k y k z k k 4 3 5 3 1 3 H 4 لبكن P أحد المستوين الموازيين ل ABC و المماسين ل S معادلة P هي على شكل xyzm m 0 لتكن d مسافة عن P لدينا d R و 120 1 1 3 3 m m أو m d R 1 3 وباتالي فإن المستويين الموازيين ل ABC و المماسين ل S هما 1 2 1 3 0 1 3 0 Px y z Pxyz الثاني التمرين 2 3 3 2 2 3 0 E z z iz i - a 1 2 3 22 3 i i هو E مميز -b 2 E ل إذن 22 3 3 0 i i S ab وبالتالي b i 3 2 وa i هما مختلفين حلين 2 - a 2 6 b 2 3 و 3 c C c 3 3 i و B 3 b i و A 2 a i إنشاء - b - a 3 3 13 1 3 22 3 ba i i c a i b - نستنتج أن المثلت ABC متساوي الأضلاع c a 3 3 2 3 i i i b - a 4 AC OB إذن c a b 0 لدينا - b JJJJG JJJG ABC المثلت ولدينا متساوي الأضلاع ومنه فإن الرباعي OBCA معين التمرين الثالث 2 1 5 4 A A 5 4 4 80 هو الممكنة النتائج عدد 1 2 عدد النتائج التي تكون فيها الكرات الثلاث تحمل الرقم0 هو 2 1 3 2 A A 3 2 2 12 3 عدد النتائج التي يكون فيها مجموع أرقام الكرات الثلاث يساوي2هو 21 111 111 AAAAAAAA 2 2 232 322 28 التمرين الرابع 1 10 1 110 0 1 1 0 1 1 1 1 2 x xx x x e dx e dx e dx xe e x e e 2 2 2 1 ln ln ln ln ln ln2 e e e e e x dx dx xx x e x ليكن - a 2 4 3 x 2 2 2 2 1 cos sin sin sin x x x x 2 2 2 2 2 2 2 2 cos sin cos cos 1 tan sin tan cos x x x x x x x x - b 2 3 3 2 2 4 4 3 3 2 4 4 1 tan sin tan tan 1 1 1 tan tan 3 dx x dx x x x dx x x

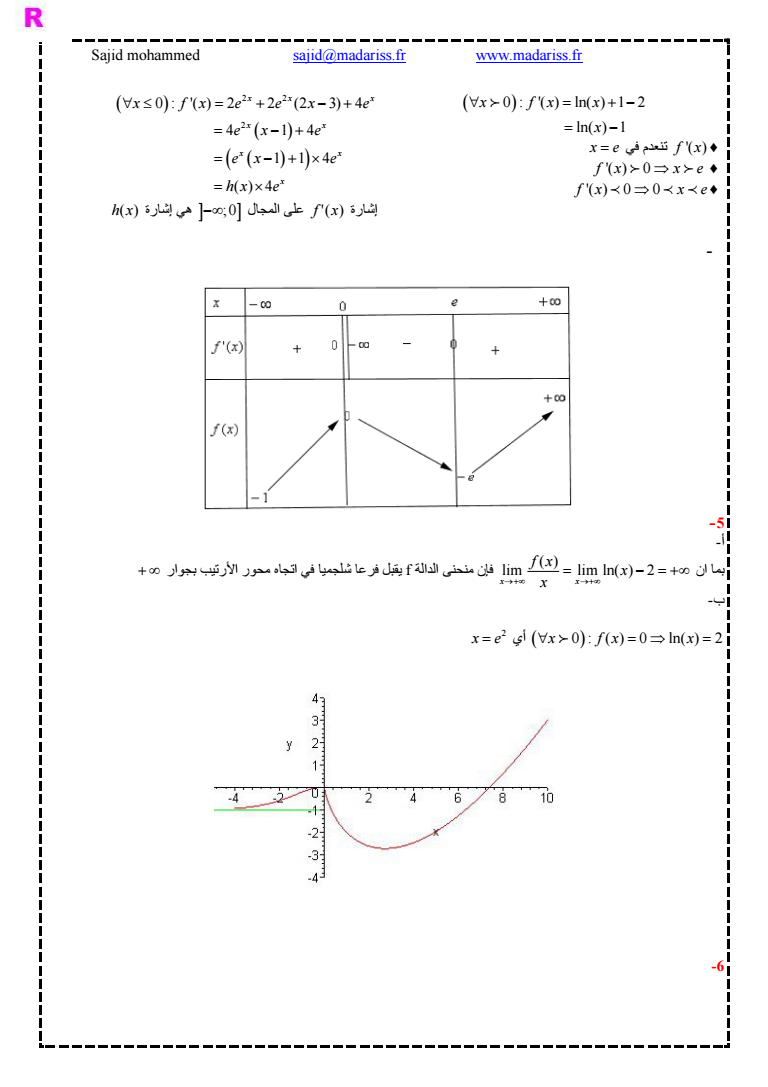
3 1 1 1 2 1 cos ln sin ln n 1 1 cos ln e e e e e J x x x x dx x e x dx e K K x x x x dx x K J إذن Je J اليوبالت e J هومن 1 1 2 1 sin l sin ln 1 1 1 مسألة الجزء الأول lim lim 1 1 x x x gx e x و 1 lim lim 1 x x x e gx x x x - a 2 x x gx e 1 b 0 - c بما أن قيمة دنبا مطلقة للدالة g عند 0 فإنه x gx gt 0 لدينا x 1 2 h x gx x بحيث h الدالة نعتبر 3 12 2 0 1 2 0 x x hx e h h gt lt 1 2 h 0 إذن وبالتالي للمعادلة x gx x حل وحيد في المجال 12 الجزء الثاني 1 و Df 1 1 lim lim 1 1 x x x fx e x lim lim ln 1 و x fx e x x x إذن f 0 1 لدينا 2 1 2 2 0 0 0 00 2 0 1 lim lim lim ln lim 2 ln 0 x x xt x xt t t fx f e t x x t t lt ltgt gt 0 t و 0 0 0 0 0 ln 1 1 lim 1 1 ln 1 1 1 0 x x x x x fx f e x x x e x x gt gt lim lim x x x x e x gt نستنتج جبريا أن fقابلة للإشتقاق في 0 و أن f 0 0 يقبل في 0 مماس معادلته Cf y f 0 و نستنتج هندسيا أن y 1 أي - a 3 0 ln 1 1 1 1 1 1 1 1 x x x x x x x x fx e x e e e x x e x e gx e x x -b 1 1 11 2 23 1 0 1 1 11 1 1 x x xx x fx e x e e ex x xx x بماأنx lt 0 فإن 1 3 1 0 x e x gt إذن إشارة f x هي إشارةx 1 -c a 4 ln 1 lim lim 1 ln 1 1 lim 1 0 1 x x x x x fx e x x x x xe x x -b يقبل فرعا شلجميا في اتجاه محور Cf الأفاصيل يقبل مقارب أفقي بجوار معادلته هي 1 Cf y -c 5 1 1 1 ln 1 1ln 1 1 2ln2 x x e x dx ex x x e

الجزء الثالث 1 ln 2 1 0 0 ln2 1 ln2 2 ln2 1 1 ln2 U gU e U لأن 0 lt1 ln2 ln2 1 lt ltlt فإنln2 1 lt و1 2 lt lt بماأن فإن وبالتالي 1 0 0 ltltlt U U 0 أن من n على بالترجع نبين 2 ltU n lt أساس الترجع 0 lt lt U 0 و ذلك حسب السؤال السابق فرضية الترجع ليكن n نفترض أن 0 ltU n lt و نبين أن 1 0 ltUn lt نعلم أن g تزايدية قطعا على إذن بالخصوص على 0 0 أن وبما إن حيث و g gU g 0 lt lt n فإن ltU n lt 0 ltUn 1 lt فإن g U n n U 1 و g و g 0 0 lt lt n U 0 n خاتمة أن n على بالترجع نبين 3 1 0 ltU U n n lt lt 1 السؤال حسب وذلك 0 ltltlt U U 1 0 الترجع أساس و 0 ltU U n n 1 lt lt أن نفترض n ليكن الترجع فرضية 0 أن نبين lt lt U U n n 2 1 lt نعلم أن g تزايدية قطعا على 0 إذن نستنتج من الإفتراض أن فإن بالتالي و g gU gU g 0 lt ltlt n n 1 2 1 0 lt lt U U n n lt n UU lt ltlt 0 n n 1 خاتمة U n إذن المتتالية تناقصية لدينا 0 المجال نعتبر 4 g g 0 0 وحيث على قطعا تزايدية و متصلة g g إذن g فإن إذن 0 ltU 0 lt U 0 U n تناقصية و مصغورة إذن U n متقاربة l l و U n gl l بهذه المعطيات نستنج أن نهاية تحقق و بما أن 0 و هما الحلين الوحيدين في للمعادلة gl l و l 0 فإن تناقصية U n lim 0 n خاتمة n U

الإمتحان التجريبي لنيل شهادة الباكا لو يا الصفحة 1 3 دورة بريل 2006 مدة الإ نجا 3 ساعات لمادة الرياضيات الشعبة علوم تجريبية المؤ سسة ثانوي المختار لسوسي-المعازيز-نيابة الخميسات المعامل 7 التمرين الأول 25ن n u نعتبر المتتالية 4 9 4 1 4 1 n n u u u k n n عدد حقيقي ثابث غير رتبط بالعدد v n المتتالية المعرفة بما يلي n v u k لتكن أحسب 1 n1 بدلالة v n بدلالة u n v v متتالية هندسية 2 n حدد k بحيث تكون ايتي حدد 3 n و u n v التمرين الثاني 25 ن الفضاء E منسوب على معلم متعامد ممنظم Oi jk نعتبر النقط الآتية C021 و B113 و A202 AB AC أحسب 1 2 حدد معادلة ديكارتية للمستوى ABC 3 أعط معادلة ديكارتية للفلكة S التي مركزها A تقطع ABC حسب الدائرة التي مركزها B و شعاعها 2 التمرين الثالث 35ن نعتبر صندوق يحتوي على ثلاث كرات صفراء كرتين زرقاوتين كرة حمراء أربع كرات خضراء لايمكن التمييز بين الكرات باللمس نسحب عشوائيا كرة من الصندوق 1 - أحسب إحتمالات الأحداث التالية J quot سحب كرة صفراء quot B quot سحب كرة زرقاء quot R quot سحب كرة حمراء quot V quot سحب كرة خضراء quot 1ن ن05 1ن 1ن ن05 1ن 1ن

2 3 2 - نعتبر الآن السحب مرتبط بربح عدد من الدراهم حسب الشروط التالية - كانت الكرة المسحوبة حمراء نربح 10 دراهم - كانت الكرة المسحوبة خضراء نربح درهمان - كانت الكرة المسحوبة صفراء أو زرقاء نربح 3 دراهم ليكن X المتغير العشوائي الذي يربط كل سحبة بعدد الدراهم المربوح - حدد قانون إحتمال المتغير العشوائي X - أحسب الأ مل الرياضي EX المغايرة VX التمرين الرابع 3ن 8 24 32 0 التالية المعادلة C نعتبر 3 2 E z z z z0 حل للمعادلة E حدد الأعداد a و b و c بحيث تكتب على شكل 1 - تأكد من أن 4 4 0 2 E z az bz c نرمز E المعادلة حل - 2 1 و z 2 Im 0 بحيث المعادلة لحلي بحيث z Im z2 0 و z1 z 2 z و 1 حدد الشكل الأسي النقط أن بين 3 2 1 0 دائرة إلى تنتمي z2 z1 z0 التوالي على لواحقها التي M M M R 2 شعاعها 2 اللحق ات مركزها مسأ لة 85 الجزء الاول 1 نعتبر الدالة f للمتغير لحقيقي x المعرفة بما يلي ln 1 2 x x x f x 1 - حدد Df مجموعة تعريف الدالة f لدينا Df - بملاحظة أنه لكل x ينتمي 1 2 1 ln 1 x x x x f x أحسب اية f على اليمين عند النقطة 1 - - رس الدالة f لنهايات - التغيرات Oi j f للدالة الممثل المنحنى C ليكن 2 - بين للمنحنى C نقطة نعطاف حدد إحداثيتيها - أكتب معادلتي المما سين للمنحنى عند النقطة التي فصولها 2 - عند النقطة I - رس الفرع اللا ائي للمنحنى C 1ن ن15 1ن 1ن 1ن ن025 ن05 1ن ن05 ن05

33 ln2 07 C أنشئ - 3 آستنتج مما سبق إشارة f x عندم يتغير x على Df الجزء الثاني نعتبر الدالة g للمتغير الحقيقي x المعرفة بما يلي 1 0 1 2 ln 1 g g x e x x x 1 1 ln 1 - بين نه لكل عدد حقيقي x مختلف عن 1- لدينا 1 x x g x x e - بين أن الدالة g متصلة عند النقطة 1 - - أدرس آشتقاق الدالة g عند النقطة 1 - 2 رس لدالة g النهايات التغيرات من أجل دراسة تغيرا يمكن آستعمال 3 من الجزء الاول uv g للدالة الممثل المنحنى ليكن 3 - درس الفروع اللاائية للمنحنى - أرسم بدون محاولة البحث عن نقطة الإ نعطاف 4 2 آستعمل لإعطاء عدد حلول المعادلة 1 1 x IR m x x m قيم حسب من إنجاز الأستاذ علي الشريف cherifalixyahoofr httparabmathssitevoilafr ن05 ن05 ن05 ن025 ن05 1ن ن05 1ن 1ن

الشعبة علوم تجريبية ثانوية المختار لسوسي المعازيز نيابة الخميسات تصحيح الإمتحان التجريبي لنيل شهادة الباكا لو يا دورة بريل 2006 n httparabmathsiftfrn من إنجاز الأستاذ علي الشريف لمادة الرياضيات cherifalixyahoofr التمرين الأول n u نعتبر المتتالية 4 9 4 1 4 1 un un u v المتتالية المعرفة بما يلي n vn un k لتكن k عدد حقيقي ثابث غير مرتبط بالعدد n حساب 1 n1 بدلالة v n بدلالة u n v لدينا v k k v u k u k n n n n 4 9 4 1 4 9 4 1 1 1 و منه 4 9 4 3 4 1 vn1 vn k v متتالية هندسية 2 n تحديد k بحيث تكون 4 من أجل ذلك يكفي أن يكون 0 9 4 3 k k 3 يعني v هندسية أساسها n إذن هذه الحالة تكون المتتالية 4 1 v0 u0 3 1 الاول حدها ايتي حساب 3 n و u n v v هندسية أساسها n بما أن 4 1 1 الاول حدها v0 فإن 0 4 1 n n يعني v v n n v 4 1 4 بما أن 1 1 lim 0 فإن 0 n n v v u k أن بما un vn k فإن n n 3 يعني n n u v lim 3 منه n n u التمرين الثاني الفضاء E منسوب على معلم متعامد ممنظم Oi j k C 021 و B 113 و A 202 النقط نعتبر AB AC حساب 1 AC 2 2 1 و AB 1 1 1 لدينا AB AC i j k إذن 2 2 1 1 2 1 1 1 2 1 1 1 AB AC 3i 3 j يعني 2 معادلة ديكارتية للمستوى ABC لدينا المتجهة AB AC منظمية على المستوى ABC ABC 3x 3y d 0 إذن d 6 فإن A ABC أن بما ABC 3x 3y 6 0 بالتالي 3 معادلة ديكارتية للفلكة S التي مركزها A تقطع ABC حسب الدائرة التي مركزها B شعاعها 2 ليكن R شعاع الفلكة r S شعاع الدائرة لدينا 2 2 2 d r R 1 1 1 3 بحيث 2 2 2 r 2 و d AB 3 4 7 منه 2 2 R d r

الشعبة علوم تجريبية ثانوية المختار لسوسي المعازيز نيابة الخميسات تصحيح الإمتحان التجريبي لنيل شهادة الباكا لو يا دورة بريل 2006 o httparabmathsiftfro من إنجاز الأستاذ علي الشريف لمادة الرياضيات cherifalixyahoofr 2 2 7 بالتالي 2 2 2 x y z 4 4 1 0 يعني 2 2 2 x y z x z التمرين الثالث نعتبر صندوق يحتوي على ثلاث كرات صفراء كرتين زرقاوتين كرة حمراء أربع كرات خضراء لايمكن التمييز بين الكرات باللمس نسحب عشوائيا كرة من الصندوق 1 - حساب إحتمالات الأحداث التالية J quot سحب كرة صفراء quot 10 3 P J B quot سحب كرة زرقاء quot 5 1 10 2 P B R quot سحب كرة حمراء quot 10 1 P R V quot سحب كرة خضراء quot 5 2 10 4 P V 2 - نعتبر الآن السحب مرتبط بربح عدد من الدراهم حسب الشروط التالية - كانت الكرة المسحوبة حمراء نربح 10 دراهم - انت الكرة المسحوبة خضراء نربح درهمان - كانت الكرة المسحوبة صفراء أو زرقاء نربح 3 دراهم ليكن X المتغير العشوائي الذي يربط كل سحبة بعدد الدراهم المربوحة - حدد قانون إحتمال المتغير العشوائي X X 2310 لدينا 5 إذن 2 P X 2 P V 2 1 5 1 10 3 3 P X P J B P J P B P J B 10 1 P X 10 P R بالتالي قانون إحتمال المتغير العشوائي X X xi 2 3 10 10 1 2 1 5 2 i P X x - حساب الأ مل الرياضي E X 10 33 10 1 10 2 1 3 5 2 2 3 1 i i i E X x P X x - حساب المغايرة V X 2 2 2 3 1 2 10 33 10 10 1 10 33 3 2 1 10 33 2 5 2 i i i V X p x E x التمرين الرابع 8 24 32 0 التالية المعادلة C نعتبر 3 2 E z z z 4 1 E للمعادلة حل z0 4 8 4 24 4 32 0 3 2 تحديد الأعداد a و b و c بحيث E تكتب على شكل 4 0 2 E z az bz c a z b z c z a z b z c a z b z c z 4 4 4 4 2 2 3 2 az b 4a z c 4bz 4c 3 2 إذن E تكتب على الشكل يعني 8 24 32 4 4 4 3 2 3 2 z z z a z b a z c b z c

الشعبة علوم تجريبية ثانوية المختار لسوسي المعازيز نيابة الخميسات تصحيح الإمتحان التجريبي لنيل شهادة الباكا لو يا دورة بريل 2006 p httparabmathsiftfrp من إنجاز الأستاذ علي الشريف لمادة الرياضيات cherifalixyahoofr 8 4 1 8 4 32 24 4 24 16 8 8 4 4 1 4 32 4 24 4 8 1 c b a c c b b a c c b b a a 4 4 8 0 بالتالي و 2 E z z z z بحيث لحلي المعادلة z 2 و 2 1 - حل المعادلة E نرمز Imz2 0 و Im z1 0 بحيث 4 4 8 0 تكافئ E المعادلة 2 E z z z 4 8 0 تكافئ 2 z 4 0 أو z z 4 8 0 2 z z 2 4 8 4 2i z 2 2i إذن z2 2 2i و 1 S 4 2 2i 2 2i هي المعادلة حلول بالتالي الأسي الشكل 1 و z 2 z 4 1 2 2 i و z e 4 2 2 2 i z e النقط 3 2 1 0 التوالي على لواحقها التي M M M 2 1 0 دائرة إلى تنتمي z z z R 2 شعاعها 2 اللحق ات مركزها 4 2 2 لدينا z1 z 2i 2 و z0 z 2 2 و z2 z i يعني أن النقط M 0 M1 M 2 هذا يكافئ أن 2 1 0 مركزها التي الدائرة إلى تنتمي M M M R 2 شعاعها 2 اللحق ات مسأ لة الجزء الاول نعتبر الدالة f للمتغير لحقيقي x المعرفة بما يلي x 1 x 1 x 2 f x ln Df IR 1 f لدالة تعريف مجموعة - 1 Df - لدينا لكل x ينتمي x 1 x 2 x 1 lnx 1 f x إذن x 1 x 2 x 1 x 1 x ln limf lim x 1 x 1 x 10 x 1 x 2 x 1 ln x 1 limx 1 limtln t 0 أن نعلم t 0 t x 1 بوضع لدينا t 0 x 1 إذن t t 1 tln t lim lim t 0 f x x 1 - الدالة f - التغيرات لنهايات limf x x limf x x limf x x 1 التغيرات f 2 x 1 x x D f x جدول التغيرات
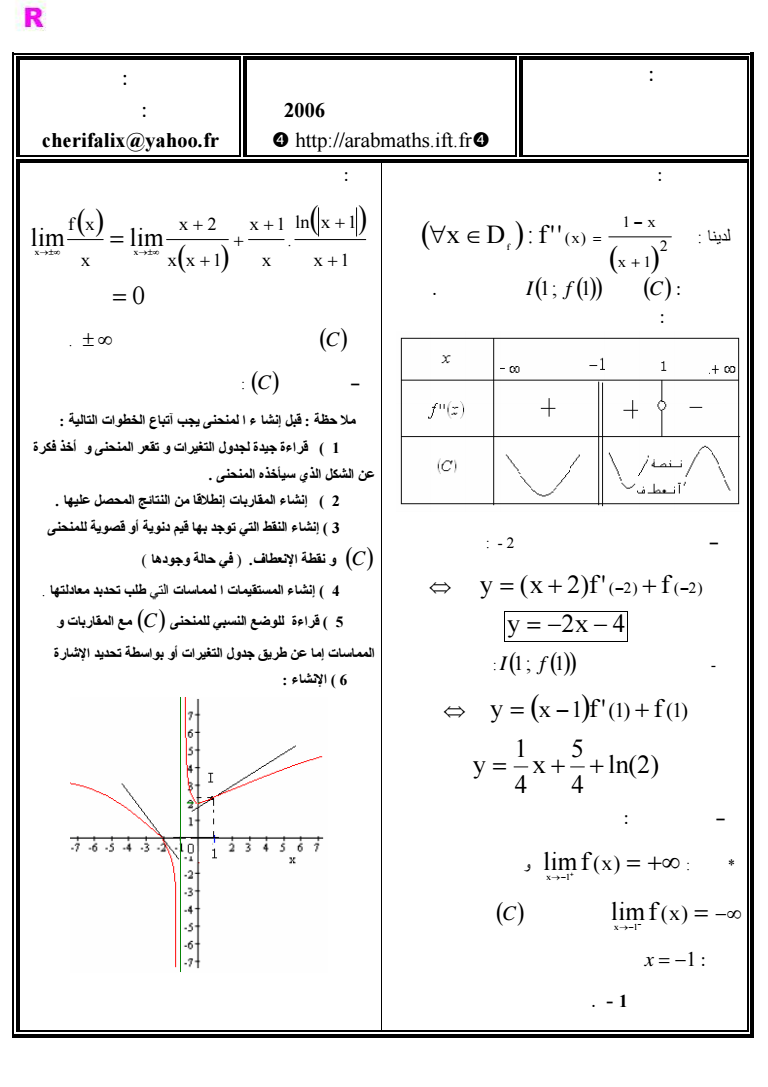
الشعبة علوم تجريبية ثانوية المختار لسوسي المعازيز نيابة الخميسات تصحيح الإمتحان التجريبي لنيل شهادة الباكا لو يا دورة بريل 2006 q httparabmathsiftfrq من إنجاز الأستاذ علي الشريف لمادة الرياضيات cherifalixyahoofr نقطة الإنعطاف لدينا 2 x 1 1 x x D fx f نستنتج أن C يقبل I1 f 1 كنقطة آنعطاف تقعر المنحنى معادلة المماس عند النقط التي أفصولها 2 - y x 2f2 f2 y 2x 4 - معادلة المماس عند النقطة I1 f 1 y x 1f1 f1 ln2 4 5 x 4 1 y الفروع اللاائية لدينا limfx x 1 و limfx x 1 هذا يعني أن C يقبل المستقيم الذي x 1 معادلته مقارب عمودي بجوار 1 - لدينا lim lim x 1 ln x 1 x x 1 x x 1 x 2 x f x x x إذ C يقبل محور الافاصيل آتجاه مقارب بجوار إنشاء المنحنى C ملا حظة قبل إنشا ء ا لمنحنى يجب آتباع الخطوات التالية 1 قراءة جيدة لجدول التغيرات و تقعر المنحنى و أخذ فكرة عن الشكل الذي سيأخذه المنحنى 2 إنشاء المقاربات إنطلاقا من النتائج المحصل عليها 3 إنشاء النقط التي توجد بها قيم دنوية أو قصوية للمنحنى C و نقطة الإنعطاف في حالة وجودها 4 إنشاء المستقيمات ا لمماسات التي طلب تحدبد معادلتها 5 قراءة للوضع النسبي للمنحنى C مع المقاربات و المماسات إما عن طريق جدول التغيرات أو بواسطة تحديد الإشارة 6 الإنشاء
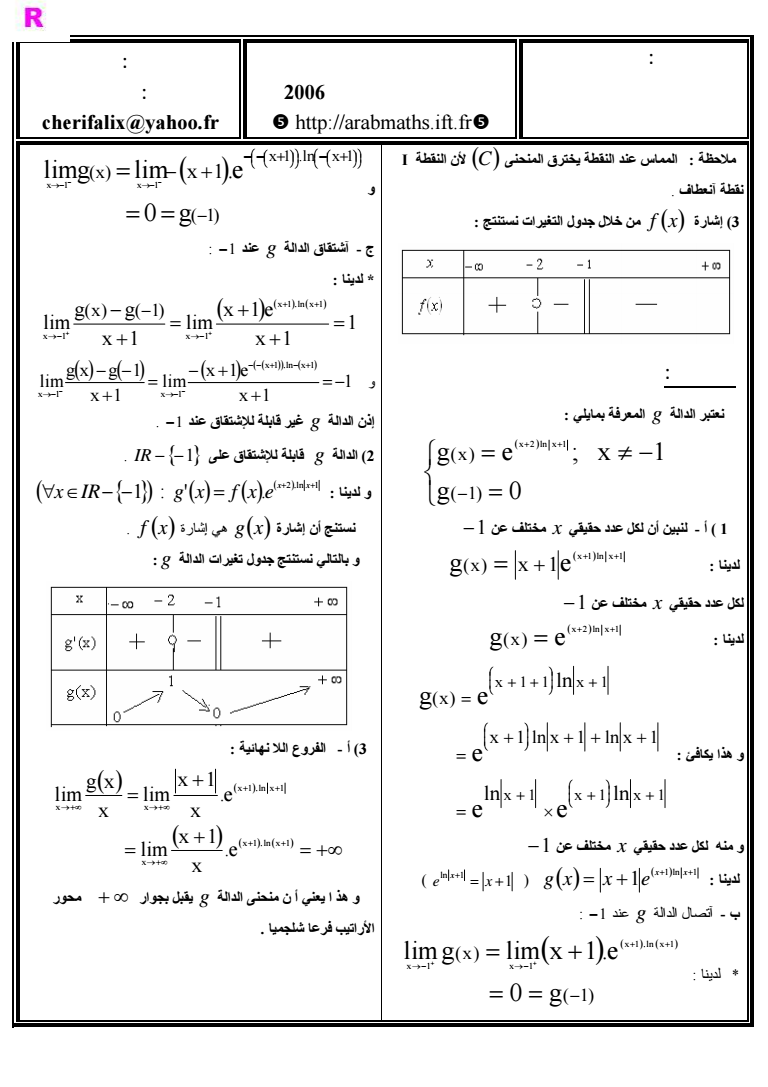
الشعبة علوم تجريبية ثانوية لمختار لسوسي المعازيز نيابة الخميسات تصحيح الإمتحان التجريبي لنيل شهادة الباكا لو يا دورة بريل 2006 r httparabmathsiftfrr من إنجاز الأستاذ علي الشريف لمادة الرياضيات cherifalixyahoofr ملاحظة المماس عند النقطة يخترق المنحنى C لأن النقطة I نقطة آنعطاف 3 إشارة f x من خلال جدول التغيرات نستنتج الجزء الثاني نعتبر الدالة g المعرفة بمايلي g 0 g e x 1 1 x x 2 ln x 1 1 أ - لنبين أن لكل عدد حقيقي x مختلف عن 1 لدينا x 1 ln x 1 gx x 1e لكل عدد حقيقي x مختلف عن 1 لدينا x 2 ln x 1 gx e و هذا يكافئ x 1 x 1 x 1 x 1 1 x 1 ln ln ln e e e g e x 1 ln x 1 ln x 1 x و منه لكل عدد حقيقي x مختلف عن 1 لدينا 1ln 1 1 x x 1 g x x e ln 1 e x x ب - آتصال الدالة g عند 1 لدينا 1 x 0 g limg lim x 1 e x 1 ln x 1 x 1 x 1 و 1 x 0 g limg lim e x 1 ln x 1 x 1 x 1 x 1 ج - آشتقاق الدالة g عند 1 لدينا 1 x 1 x 1 e lim x 1 g g lim x 1 ln x 1 x 1 x 1 x 1 و 1 x 1 x 1 e lim x 1 g x g 1 lim x 1 ln x 1 x 1 x 1 إذن الدالة g غير قابلة للإشتقاق عند 1 2 الدالة g قابلة للإشتقاق على IR 1 لدينا و 2 ln 1 1 x x x IR g x f x e نستنج أن إشارة g x هي إشارة f x و بالتالي نستنتج جدول تغيرات الدالة g 3 أ - الفروع اللا نهائية x 1 ln x 1 x x 1 ln x 1 x x e x x 1 lim e x x 1 lim x g x lim و هذ ا يعني أ ن منحنى الدالة g يقبل بجوار محور الأراتيب فرعا شلجميا
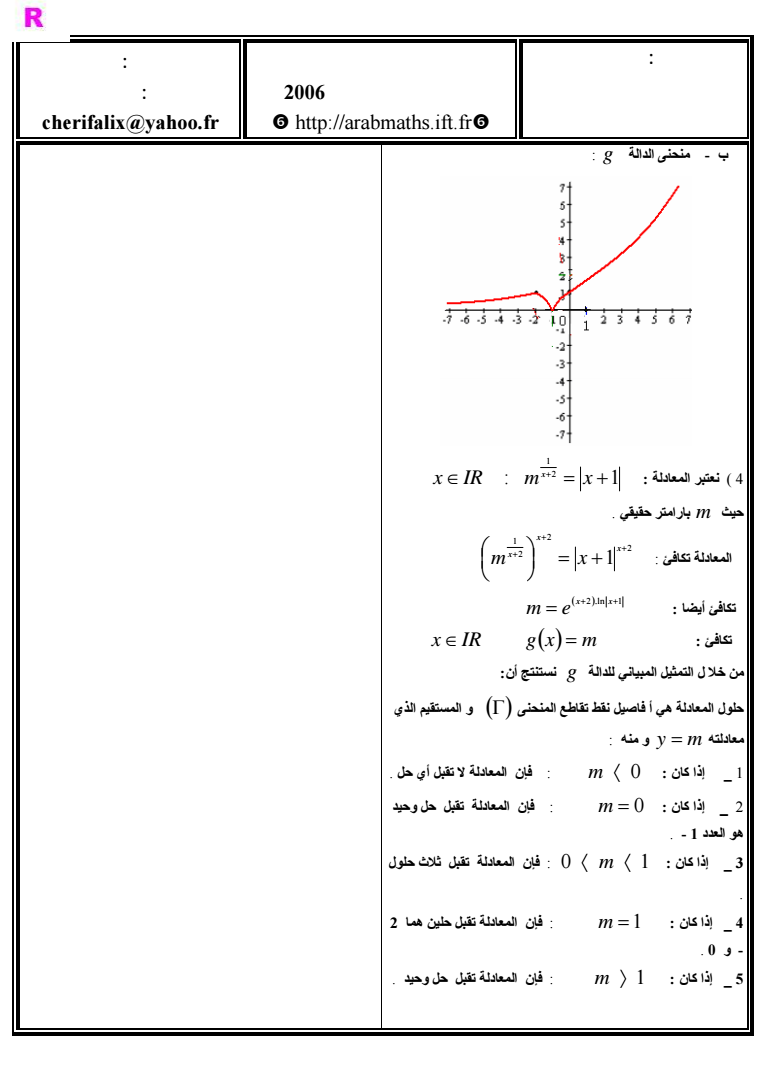
الشعبة علوم تجريبية ثانوية المختار لسوسي المعازيز نيابة الخميسات تصحيح الإمتحان التجريبي لنيل شهادة الباكا لو يا دورة بريل 2006 s httparabmathsiftfrs من إنجاز الأستاذ علي الشريف ادة الرياضيات cherifalixyahoofr ب - منحنى الدالة g 1 المعادلة نعتبر 4 2 1 x IR m x x حيث m بارامتر حقيقي 2 المعادلة تكافئ 2 2 1 1 x x x m x أيضا تكافئ 2 ln 1 x x m e x IR gx m تكافئ من خلا ل التمثيل المبياني للدالة g نستنتج أن حلول المعادلة هي أ فاصيل نقط تقاطع المنحنى و المستقيم الذي معادلته y m و منه 1 إذا آان m 0 فإن المعادلة لا تقبل أي حل 2 إذا آان m 0 فإن المعادلة تقبل حل وحيد هو العدد 1 - 3 إذا آان 0 m 1 فإن المعادلة تقبل ثلاث حلول 4 إذا آان m 1 فإن المعادلة تقبل حلين هما 2 - و 0 5 إذا آان m 1 فإن المعادلة تقبل حل وحيد


10 SAID BOUZAWIT - lyce Abdelali Benchakroune التمرین الأولنقطتان 1ن1- احسب التكامل التالي ln 4 ln 2 1 x e dx 1 ضع I x t e 1ن2- احسب باستعمال مكاملة بالأجزاء 1 J Arctg x dx التمرین الثاني3نقط یحتوي كیس على خمس بیدقات لا یمكن التمییز بینھا باللمسبیدقتان تحملان الرقم 0وبیدقتان تحملان الرقم1وبیدقة تحمل الرقم2نسحب عشوائیا وفي آن واحد بیدقتین من الكیس 1- لیكن X المتغیر العشوائي الذي یساوي مجموع الرقمین المسجلین على البیدقتین المسحوبتین 1ن أ- حدد قانون احتمال X 05 ن ب- لیكن A الحدثquotسحب بیدقتین تحملان نفس الرقمquot تحقق أن 10 2 p A 05 ن ج- بین أن الحدث A و الحدث X 2 غیر مستقلین 1ن 2- نكرر التجربة السابقة ثلاث مرات متتابعة وفي كل مرة نعید الكرتین المسحوبتین إلى الكیس احسب احتمال تحقیق A مرتین على الأقل التمرین الثالث 35نقط 2 1 0 المعادلة C في حل -1 ن1 2 E z z i Imz 0 حیث E المعادلة جذرا zquotو z zquot و z احسب -2ن 05 1ن 3- احسبquotzz واكتب z1 على الشكل المثلثي Argzquot و Argz استنتج -4 ن1 التمرین الرابع 25نقط الفضاء منسوب الى معلم متعامد ممنظم مباشر O i j k C001و B 211 A202 النقط نعتبر 2 2 4 3 0 المعادلة ذات Sوالفلكة 2 2 2 x y z x y z 1 ن 1- احسب AB AC واستنتج معادلة دیكالرتیة للمستوى ABC 05 ن2- حدد مركز وشعاع الفلكةS

11 SAID BOUZAWIT - lyce Abdelali Benchakroune 1ن 3- بین أنABC مماس للفلكةS و حدد نقطة التماس مسألة 9نقط نعتبر الدالة العددیة f المعرفة على IR بما یلي 1 1 1 1 2 2 3 2 x e x x x x f x x منحناھا في معلم متعامد ممنظمCf O i j ولیكن - 025 ن 1- أ- ادرس اتصال f في1- 05 ن ب- بین أن 1 x 1 f x Lim x ثم أعط تأویلا ھندسیا لھذه النتیجة 025 ن ت- بین أن f قابلة للاشتقاق في 1 ثم فسر النتیجة ھندسیا Lim f x احسب ج ن 05 x و x f x Lim x ثم أعط تأویلا ھندسیا لھذه النتیجة 0 أن بین -د ن 05 Lim f x x ثم أعط تأویلا ھندسیا لھذه النتیجة أن بین -أ -2 ن 05 3 1 1 3 1 4 3 2 2 3 2 2 x x e x x x x f x x 05 ن ب- ضع جدول تغیرات f 1 المجال من x لكل f x x أن بین -3 ن 05 Cf في النقطة ذات الأفصول05 0 ن 4 - أ- اكتب معادلة دیكارتیة للمستقیمT مماس 1 Cfن ب- أنشئ i j 2cm نأخذ T و 06 و 4 1 02 و 3 2 3 e - لیكن h قصور الدالة f على المجال 1 نعتبر Un n0 المتتالیة المعرفة كما یلي 1 0 1 0 0 U h U n U U n n أن بین -1 ن1 Un n0 تزایدیة 1 U0 0 أن نفترض -2 1 0 أن بین -أ ن 05 Un لكل n من IN أن بین -ب ن 075 Un n0 متقاربة و احسب نھایتھا 0 أن نفترض -3 U0 3 U0 1 1 التالي الحقیقي العدد لیكن و U0

12 SAID BOUZAWIT - lyce Abdelali Benchakroune أن بین -أ ن 075 Un1 Un لكل n من IN U U n أن بین -ب ن 075 IN من n لكل n 0 نھایة استنتج -ج ن 025 Un n0

25 SAID BOUZAWIT - lyce Abdelali Benchakroune التمرین الأول x ln 2 t 1 و x ln 4 t 3 1 2 t e 1 x ln 1 t x ومنھ 2 1 2 t t dt dx إذن 6 2 1 2 3 1 3 1 2 Arctg t t dt I 2 1 2 1 1 dx x x و J xArctg x 1 2 1 2 ln 1 2 1 1 ln 2 4 dx x x x J التمرین الثاني 1 أ- 0 1 2 3 i x 10 2 2 5 1 1 1 2 C C C 10 3 2 5 1 1 1 2 2 2 C C C C 10 2 2 5 1 2 1 2 C C C 10 1 2 5 2 2 C C i p X x -ب 10 2 2 5 2 2 2 2 C C C p A ج- الحدث A X 2 ھو quot سحب بیدقتین تحملان الرقم 1quot إذن 10 1 p A X 2 لدینا و 50 3 مستقلین غیر Aو X 2 الحدثان إذن p A p X 2 50 3 10 1 لدینا 2 3 3 3 2 2 إذن p C3 p A 1 p A C p A 125 13 p التمرین الثالث 1 2 1 4 2 1 2 2 1 1 2 2 zquot 1 i و z i i i 2 2 2 2 2 2 2 quot 1 2 2 z 2 2 2 2 2 2 1 2 2 z az bz c جذري جداء zzquot 1 i 3 2 یساوي a c و 4 3 1 2 2 2 2 1 z i لدینا 4 4 3 4 3 1 4 3 4 3 1 z Cos iSin z Cos iSin

26 SAID BOUZAWIT - lyce Abdelali Benchakroune إذن 8 3 8 3 2 8 3 2 2 z Sin iSin Cos 2 2 2 و Sin Sin Cos 2 1 2 2 Cos Sin یعني 8 3 8 3 8 3 2 منھ و z Sin Sin iCos 8 7 8 3 2 Arg z zzquot 1 i أخرى جھة من 4 quot Arg z z یعني 4 quot إذن Arg z Arg z 8 5 quot Arg z التمرین الرابع AB AC i 2 j 2k AB 411 و AC 201 1 ABC x 2y 2z d 0 إذن ABC على منظمیة AB AC ABC x 2y 2z 2 0 بالتالي و d 2 C ABC 1 1 2 9 لدینا 2 2 2 2 112 و r 3 إذن S x y z d ABC r 3 3 9 1 2 4 2 ABC مماس للفلكة S Habc نقطة التماس ھي المسقط العمودي للنقطة 112على ABC إذن 2 2 2 0 2 2 1 2 1 a b c c t b t a t H010 t 1 t IR مسألة -I lim 0 و f 1 0 -أ 1 1 f x f x 1 lim إذن f متصلة في 1- ب- 3 2 1 3 1 1 1 1 lim 1 1 lim 1 lim x x x x x x f x إذن f غیر قابلة للاشتقاق في 1 Cf یقبل نصف مماس عمودي موجھ نحو الأعلى في النقطة A10 على الیمین ث- 2 1 2 1 2 2 1 1 lim 1 2 1 1 lim 1 lim 2 2 x e e x x e x f x x x إذن f قابلة للاشتقاق في 1 Cf 2 یقبل نصف مماس معاملھ الموجھ 1 2 e في النقطة A10 على الیسار -ج 3 و lim f x lim x x 1 3 lim lim x 1 x f x Cf یقبل فرعا شلجمیا في اتجاه محور الأراثیب بجوار 0 -د 2 lim lim 1 lim 2 2 2 2 2 2 2 2 2 x x x e x ضع f x x e e 2 2 x t
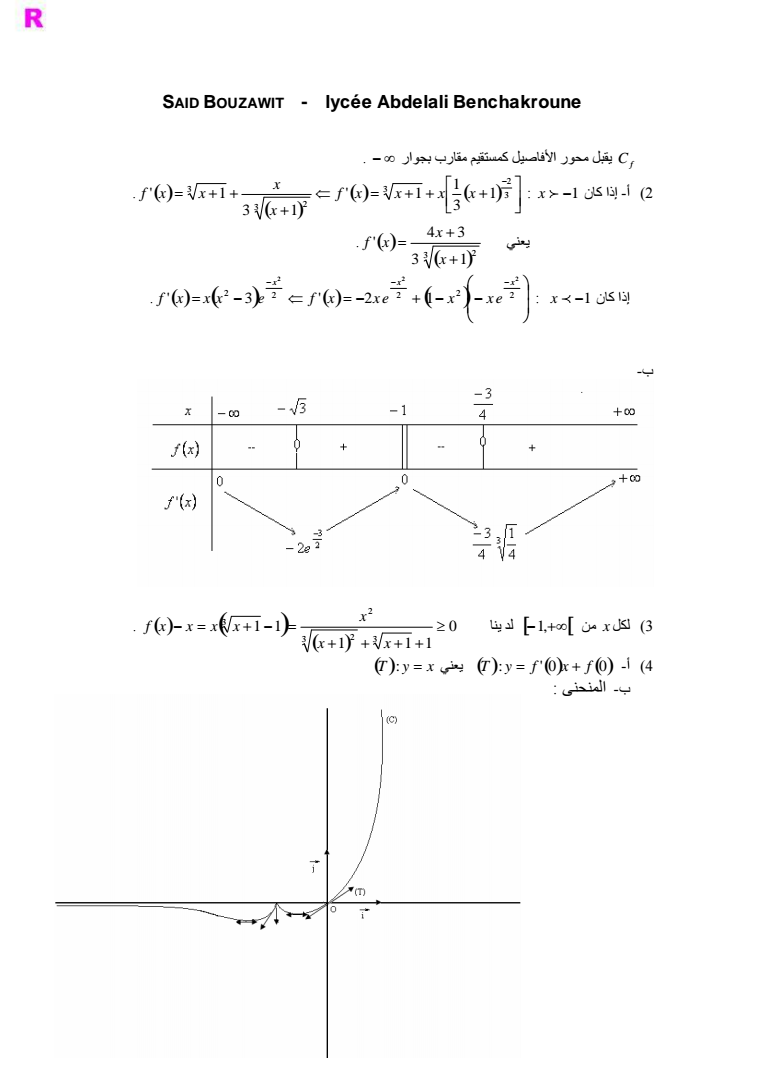
27 SAID BOUZAWIT - lyce Abdelali Benchakroune Cf یقبل محور الأفاصیل كمستقیم مقارب بجوار x 1 كان إذا -أ 2 3 2 3 3 2 3 1 3 1 1 3 1 1 f x x x x x x f x x یعني 3 2 3 1 4 3 x x f x x 1 كان إذا 2 2 2 2 2 2 2 2 3 2 1 x x x f x x x e f x x e x x e ب- ینا لد 1 من x لكل 3 1 1 1 1 1 3 2 3 2 3 x x x f x x x x T y x یعني T y f 0x f 0 -أ 4 ب- المنحنى

28 SAID BOUZAWIT - lyce Abdelali Benchakroune -II إذن Un 1 أن نفترض U0 1 لدینا 1 4 1 4 3 1 h U h 3 n یعني 1 Un 1 0 1 وبالتالي n Un Un تزایدیة إذن Un1 hUn Un نجد x Un حسب السؤال 3 من الجزء الأول وبوضع 1 0 n 0 أجل من -أ 2 1 Un 0 أن نفترض U0 10 إذن لدینا Un یعني 4 1 4 3 h U h 10 3 n 10 بالتالي و Un1 0 10 إذن n Un Un تزایدیة ومكبورة ب0 إذن فھي متقاربة ب- و hI I و I على متصلة h I 10 نضع Un متقاربة إذن نھایتھا l تحقق hl l 1 1 0 أي 3 l 0 ومنھ l l 1 1 لدینا -أ 3 3 Un تزایدیة إذن وبما أن U0 0 Un U0 و Un1 Un Un Un 1 1 نجد 3 IN من n لكل Un1 Un U0 U0 Un U0 n أن نفترض محققة العلاقة U0 U0 ب- من أجل n 0 لدینا و Un1 Un إذن U U n n 1 0 1 أي Un1 U0 n U U n إذن IN من n لكل n 0 limUn منھ و limU0 n إذن 0 لدینا -ج

2 -1- W 3 W 7 W 2006 W 1 أحسب التكامل التالي 1 2 2 0 1 x I dx x 2 باستعمال المكاملة بالأجزاء أحسب التكامل ln 2 x J xe dx W التالية المعادلة في نعتبر 2 Ez i z i 2 13 13 130 أن تحقق 1 1 الآخر الحل واستنتج E للمعادلة حل z i 1 2 E للمعادلة z z على شكليهما المثلثي z 2 و 2 1 أآتب نضع 3 1 2 z Z z 7 أآتب Z على الشكل الجبري والمثلثي واستنتج قيمتي cos 12 و 7 sin 12 W نعتبر النقطتين A 2 10 و Oi jk JG JJG JJG في الفضاء المنسوب إلى معلم متعامد ممنظم ومباشر Q xy z 2 2 3 0 و P xyz 10 والمستويين B 301 1 أعط تمثيلا بارامتريا للمستقيم المار من النقطة A والعمودي على المستوى Q 2 بين أن المستويين P و Q متقاطعين وفق مستقيم D ثم حدد تمثيلا بارامتريا له 3 حدد معادلة ديكارتية للمستوى R المار من النقطة B والعمودي على المستويين P و Q R 3 وشعاعها 113 مرآزها فلكة S لتكن 4 أ- أعط معادلة ديكارتية للفلكة S ب- بين أن المستوى P يقطع الفلكة S وفق دائرة محددا مرآزها وشعاعها 2 ن 1 1 35 ن 1 1 15 45 ن 1 1 1 05 1

2 -2- W نعتبر الدالة العددية f للمتغير الحقيقي x المعرفة على بما يلي 2 ln 3 2 2 2 fx x x x fx x x x x gt المنحنى الممثل للدالة العددية f في المستوى المنسوب إلى معلم متعامد ممنظم Cf و نعتبر Oi j JJG JJG 1 أ- أحسب lim x f x lim و x f x ب- أدرس اتصال الدالة f في النقطة 2 وأن f g 2 أ- بين أن 2 0 2 2 limx 2 fx f x ب- أعط تأويلا هندسيا للنتيجتين السابقتين و 3 2 بين أن f تزايدية قطعا على آل من المجالين 2 يقبل مقاربا مائلا بجوار معادلته y x 2 1 وأن المستقيم ذو المعادلة 4 Cf بين أن المنحنى بجوار y x Cf اتجاه مقارب للمنحنى أنشئ 5 Cf 6 ليكن g قصور الدالة f على المجال 2 نحو مجال J يجب تحديده أ- بين أن g تقابل من المجال 2 لكل x من المجال 1 g x J ب- حدد المعرفة بما يلي 7 n u نعتبر المتتالية العددية n 1 1 ln 3 n n n u uu u n 0 2 أن بين -أ n u lt n تزايدية n n u ب- بين أن المتتالية متقاربة ثم أحسب نهايتها n n u ج- استنتج أن ltltcltje lt 10 ن 05 1 1 05 15 1 15 05 05 05 05 1

- 1 - الأستاذ الحيان 1 1 تصحيح الامتحان التجريبي 27 أبريل 1 2006 1 الثانية بكالوريا علوم تجريبية 1 1 التمرين الأول quot 1 لدينا 1 1 1 11 2 2 22 2 2 0 0 0 00 11 1 1 1 11 1 1 x x I dx dx dx dx dx xx x x 1 0 1 tan 1 4 I Arc x وبالتالي فإن 1 2 2 1 1 4 x I dx x نضع 2 x ux e vx x 1 إذن x ux e v x دالتين و v دالتين قابلتين للاشتقاق على المجال 0ln 2 و u v و لدينا u متصلتين على المجال 0ln 2 حسب المكاملة بالأجزاء لدينا ln 2 ln 2 ln 2 ln 2 ln 2 0 0 0 00 x x J u x v x dx u x v x u x v x dx xe e dx ln 2 ln2 ln2 0 ln2 0 2ln2 1 2ln2 1 x Je e e وبالتالي فإن ln 2 2ln2 1 x J xe dx التمرين الثاني quot نعتبر في المجموعة المعادلة 2 Ez i z i 2 13 13 130 لدينا 1 2 1 2 13 1 13 13 ii i i 2 22 1 3 1 31 3 1 3 0 i ii i حل للمعادلة E ليكن 1 إذن z 1 i 2 E للمعادلة الآخر الحل z أن نعلم 1 2 2 13 2 13 1 i b zz i a إذن 2 1 zi i 2 13 2 1 z i 3 1 1 i 3 لدينا 2 2 2 1 إذن z 112 1 22 5 2 2 2 22 4 4 z i ولدينا 2 2 z إذن 2 1 32 2 13 2 2 2 2 22 3 3 z i هو Z الشكل ألمثلثي ل 3 1 2 5 2 4 25 2 27 2 2 4 3 2 12 2 3 z Z z هو Z والشكل الجبري ل 1 2 1 13 1 1313 1 3 1 31 3 4 4 i i z i Z i z i i i ومنه نستنتج أن 2 7 13 cos 2 12 4 2 7 13 sin 2 12 4 إذن 7 cos 12 7 sin 2 6 4 2 12 6 4 التمرين الثالث quot في الفضاءE المنسوب إلى معلم متعامد ممنظم Oi jk G نعتبر JG JG B 301 و A 2 10 النقطتين Q xy z 2 2 30 و P xyz 10 والمستويين والعمودي على المستوى Q 1 ليكن المستقيم المار من النقطة A u 212 لدينا إذن G متجهة منظمية على المستوى Q ولدينا Q

- 2 - u نقطة من الفضاءE G متجهة موجهة للمستقيم لتكن M xyz لدينا AM JJJJG u و G M مستقيميتان t AM t u JJJJG G 2 2 1 0 2 x t y tt z t 2 2 1 2 x t y tt z t هذه النظمة هي تمثيل بارامتري للمستقيم u 212 لدينا 2 G متجهة منظمية على المستوى Q و v 111 G متجهة منظمية على المستوى P ولدينا 11 21 21 21 21 11 uv i j k i k G G GJG JG G JG G إذن u G v و G Q متجهتان غير مستقيميتان ومنه فإن المستويين P و u v 101 بالمتجهة موجه D مستقيم وفق متقاطعان G G معادلتين هما له ديكارتيتين 1 0 2 23 0 xyz xy z z مثلا نجد من أجل 1 2 50 x y x y إذن 2 50 y x x x 5 ومنه فإن 5 y x تنتمي إلى المستقيم D C 551 النقطة فإن وبالتالي نقطة من الفضاءE لدينا M xyz لتكن CM JJJJG u v و G G M D مستقيميتان t CM t u v JJJJG GG 5 5 0 1 x t MD y t z t 5 5 1 x t y t z t هذه النظمة هي تمثيل بارامتري للمستقيم D D هو تقاطع المستويين P و Q Q العمودي على المستويين P و و ليكن R المستوى المار من النقطة B 3 u v 101 أن وبما D المستقيم على عمودي R إذن G G متجهة موجهة للمستقيم D فإنها متجهة منظمية على المستوى R نقطة من الفضاء E لدينا M xyz لتكن 3 10 2 0 M R BM u v x z x z JJJJG G G وبالتالي فإن معادلة ديكارتية للمستوى R هي x z 2 0 R وشعاعها3 113 مرآزها التي الفلكة S لتكن 4 نقطة من الفضاء E لدينا أ- لتكن M xyz 2 2 222 2 22 1 1 39 2 2 6 20 M S MR M R xyz xyz x yz لدينا -ب 222 1131 4 43 111 3 3 dP R lt إذن التي المستوى P يقطع الفلكة S وفق الدائرة C r
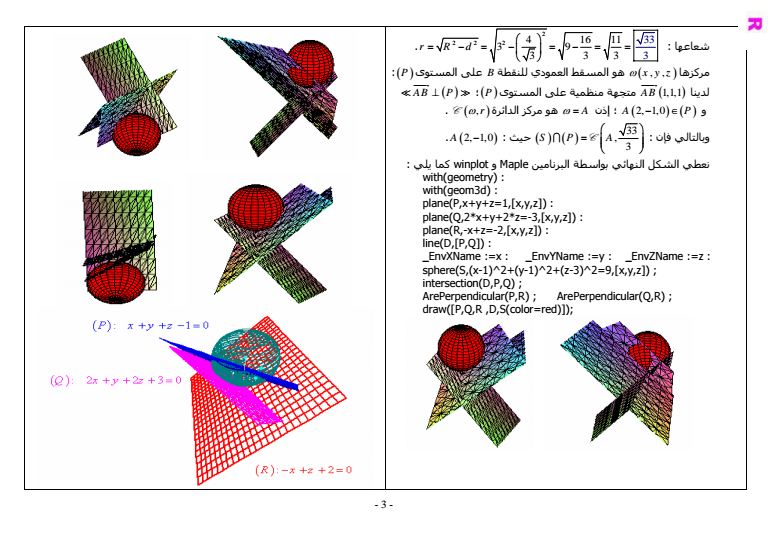
- 3 - شعاعها 2 22 2 4 16 11 3 9 3 33 3 3 3 r Rd مرآزها x y z هو المسقط العمودي للنقطة B على المستوى P AB 111 لدينا JJJG متجهة منظمية على المستوى P AB P JJJG C r الدائرة مرآز هو A إذن A 2 10 P و فإن وبالتالي 33 3 SP A A 2 10 حيث C نعطي الشكل النهائي بواسطة البرنامين Maple و winplot آما يلي withgeometry withgeom3d planePxyz1xyz planeQ2xy2z-3xyz planeR-xz-2xyz lineDPQ EnvXName x EnvYName y EnvZName z sphereSx-12y-12z-329xyz intersectionDPQ ArePerpendicularPR ArePerpendicularQR drawPQR DScolorred

- 4 - quotالتمرين الرابع نعتبر الدالة العددية للمتغير الحقيقي x المعرفة على R بما يلي 2 ln3 2 2 2 fx x x x fx x x x x gt لدينا -أ 1 ln lim lim ln3 lim 3 ln lim 3 1 xx t t t fx x x t t t t lim x f x x t ولدينا t x 3 حيث ولدينا 2 2 2 lim lim 2 lim 1 xx x fx x x x x x x 22 2 lim lim 1 lim 1 lim 1 1 xx x x fx x x x x x x x x lim x f x 2 ب- لدينا 2 2 lim lim 2 2 x x fx x x x و 2 2 lim lim ln3 2 ln1 2 x x fx x x f 2 2 و بما أن 2 2 lim lim 2 x x fx fx f فإن f متصلة في النقطة 2 2 أ- لدينا 2 2 2 ln3 2 lim lim x x 2 2 fx f x x x x x t 2 1 إذن t x 3 نضع فإن منه و 2 11 2 1 ln ln lim lim lim1 1 1 2 1 x tt 1 fx f t t t x tt g f إذن f قابلة للاشتقاق على اليسار في النقطة 2 ولدينا 2 0 لدينا 2 2 22 2 2 2 2 2 lim lim lim 1 xx x 22 2 f xf x x x x x xx x 2 22 2 2 2 2 2 lim lim 1 lim 1 2 2 2 2 xx x fx f x x x x x xx xx إذن f غير قابلة للاشتقاق على اليمين في النقطة 2 ب- لدينا f قابلة للاشتقاق على اليسار في النقطة 2 و f g2 0 إذن يقبل نصف مماس على اليسار في النقطة التي أفصولها 2 معادلته Cf 2 2 2 2 g yf x f x أي 22 g yx T 2 0 و f 2 2 g f لدينا 2 2 lim x 2 fx f x رأسي Cf يقبل نصف مماس موجه إذن نحو الأعلى على اليمين في النقطة التي أفصولها 2 لدينا x 2 ليكن 3 2 2 2 22 2 2 2 1 2 1 1 1 0 22 22 2 xx x x f x xx x xx xx xx gt إذن f تزايدية قطعا على المجال 2 ليكن x 2 لدينا 3 1 2 ln3 1 1 0 3 33 x x f xx x x xx gt إذن f تزايدية قطعا على المجال 2
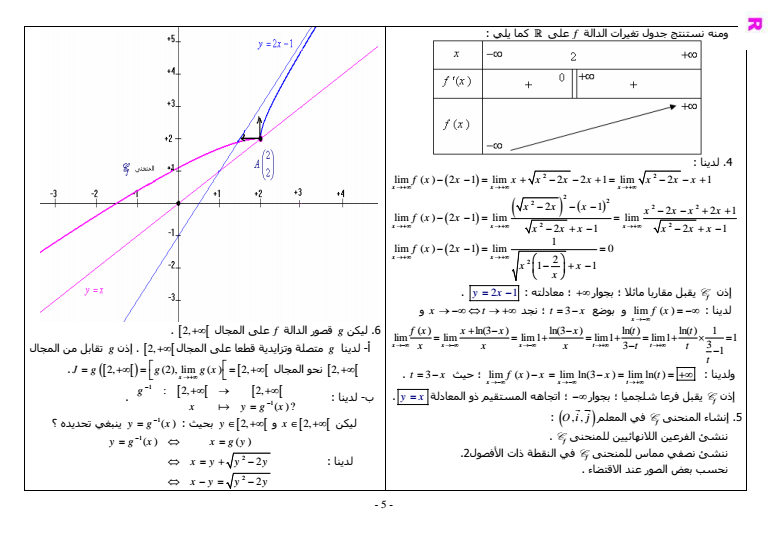
- 5 - ومنه نستنتج جدول تغيرات الدالة f على R آما يلي 4 لدينا 2 2 lim 2 1 lim 2 2 1 lim 2 1 xx x fx x x x x x x x x 2 2 2 2 2 2 2 2 1 2 21 lim 2 1 lim lim 21 21 xx x xx x x xx x fx x x xx x xx 2 1 lim 2 1 lim 0 2 1 1 x x fx x x x x يقبل مقاربا مائلا بجوار معادلته Cf y x 2 1 إذن لدينا lim x f x و بوضع t x 3 نجد x t و ln3 ln3 ln ln 1 lim lim lim 1 lim1 lim1 1 3 3 1 xx x t t fx x x x t t x x x tt t lim lim ln3 lim ln ولدينا x xt fx x x t t x 3 حيث يقبل فرعا شلجميا بجوار اتجاهه المستقيم ذو المعادلة Cf y x إذن Oi j المعلم في Cf المنحنى إنشاء 5 G JG Cf ننشئ الفرعين اللانهائيين للمنحنى Cf في النقطة ذات الأفصول2 ننشئ نصفي مماس للمنحنى نحسب بعض الصور عند الاقتضاء 6 ليكن g قصور الدالة f على المجال 2 أ- لدينا g متصلة وتزايدية قطعا على المجال 2 إذن g تقابل من المجال 2 2 lim 2 المجال نحو 2 x J g g gx لدينا -ب 1 1 2 2 g x ygx 6 ينبغي تحديده 1 ygx ليكن x 2 و y 2 بحيث لدينا 1 2 2 2 2 y g x x gy x yy y x yy y
- 6 - 2 1 2 2 22 2 2 2 2 2 2 2 2 2 2 2 1 ygx xy y y x xy y y y x xy y x xy x y x وبالتالي فإن 1 2 2 2 2 1 g x x x 6 7 نعتبر المتتالية العددية un n المعرفة بما يلي 1 1 ln3 nn n n u u u u fu n لدينا n 0 أجل من -أ 0 إذن u 1 0 0 2 ltu 0 2 أن نفترض n ليكن n ltu 0 2 ltun 1 أن نبين لدينا f تزايدية قطعا على المجال 0 2 إذن 1 1 0 2 0 2 0 ln2 2 0 2 n n nn u f fu f u u lt lt lt lt lt 0 2 فإن وبالتالي n n u lt أن وبما uu u nn n 1 ln 3 لدينا n ليكن -ب 0 2 2 0 13 3 nnn uu u nn n 1 ln 3 0 فإن ltuuu lt lt تزايدية n n u ومنه فإن المتتالية العددية ج- لدينا un n تزايدية ومكبورة بالعدد 2 إذن un n متتالية متقاربة 0 2 ولدينا n n u f دالة متصلة على المجال0 2 f بالدالة مستقر 0 2 f 02 ln22 02 un n متتالية متقاربة نهايتها l f ln 3 ln 3 0 3 1 2 l l ll l l l l إذن lim 2 فإن وبالتالي n n u بالتوفيق إنشاء االله

الموضوع 12 المستوى الثانیةمنسلك البكالوریا الشعبة العلومالتجریبیة مادة الریاضیات مدةالإنجاز 3ساعات ثانویةدمناتالتأهیلیة دمنات -أزیلال امتحانالبكالوریا الامتحانالتجریبيالموحد دورةأبریل 2007 سلم التنقیط 025 05 025 05 1 025 05 1 1 025 05 05 05 05 05 075 025 05 075 یسمحباستعمالالآلةالحاسبةغیرالمبرمجة التمرینالأول 25ن A111 النقطةOi j k المنسوبإلىمعلممتعامدممنظممباشرنعتبرفيالفضاء x y z 2 0 الذيمعادلتهP والمستوى P والعموديعلىالمستوىA المارمنالنقطةD حددتمثیلابارامتریاللمستقیم-1 P والمستوىD نقطةتقاطعالمستقیمB حددإحداثیات-2 r 7 وشعاعهاA التيمركزهاS نعتبرالفلكة-3 أ-أعطمعادلةدیكارتیةللفلكة S ب-بینأنالمستوى Pیقطعالفلكة Sوفقدائرة Cمحددامركزهاوشعاعها S والمماسینللفلكةP حددمعادلتيالمستویینالموازیینللمستوى-4 التمرینالثاني 35ن Pz z 3 22 3iz 2 415iz 161i حیثPz الحدودیةC نعتبرفي P جذرللحدودیةz0 2 تحققأن-أ-1 Pz z z 0 z 2 az b بحیثb وa حددالعددینالعقددیین-ب E Pz 0 المعادلةC حلفي-ج ez 2 0 حیثE الحلینالآخرینللمعادلةz 2 وz1 لیكن-2 بینأنحلولالمعادلة Eهيحدودمتتابعةمنمتتالیةهندسیةحدهاالأول u0 z0ثم u16 حددأساسها qوالحد C4iوB2 2i وA2 مثلفيالمستوىالعقديالنقط-أ-3 C1 وB1 وA1 مرجحالنقطالمتزنةG حددلحقالنقطة-ب التمرینالثالث 35ن x n e x dx نضعn IN منأجل 1 I n I 1 باستعمالمكاملةبالأجزاءاحسب-1 1منn بینأنلكل-أ-2 IN e I nI n n 1 1 I ب-احسب I 2و 3 2x 4x e x ج-احسبالتكامل dx 1 3 2 بینأنالمتتالیة-أ-3 n n IN I تناقصیةومصغورةبالعدد Iمتقاربة n ب-استنتجأن nIN 1 ج-بینأنلكل nمن IN 1 n n ثماستنتجI n n lim مسألة 105ن الجزءالأول gx x1 ln x الدالةالعددیةالمعرفةبمایليgلتكن lim احسب-1 g x x x lim gx و

22 المستوىالثانیةبكالوریا الشعبةعلومتجریبیة الامتحانالتجریبيالموحد مدةالإنجاز 3ساعات ثانویةدمناتالتأهیلیة دورةأبریل2007 05 025 05 05 05 025 15 1 025 1 1 1 05 05 05 منx لكلgx احسب-2 g ثمأعطجدولتغیراتIR 3-استنتجأنلكل xمن gx 0 IR نعتبرالدالةالعددیة fللمتغیرالحقیقي xالمعرفةعلى0بمایلي الجزءالثاني 0 0 ln 1 f f x e x x x x cمنحناهافيمعلممتعامدممنظم f ولیكن lim f x واحسب0 علىالیمینفيالنقطةf ادرساتصالالدالة-1 x 2-أ-تحققأن ln 1 x x e x f x 0منالمجالx لكل ب-ادرساشتقاقالدالة fعلىالیمینفيالنقطة 0ثمأولالنتیجةهندسیا ج-احسبالنهایة x f x x lim د-بینأن 1 ln lim x f x x x یمكنكاستعمالالنتیجة 1 1 lim t e t t f ثمحددالفرعاللانهائيلمنحنىالدالةx lim f x x استنتجأن f ثمادرسإشارتهاوأعطجدولتغیراتالدالة0منالمجالx لكلf x احسب-3 f 3 وf 2 وf 1 احسب-أ-4 c f ب-أنشئالمنحنى 3 43 نعطي 3 4 A11 نقطةانعطاففيالنقطc f ونقبلأنللمنحنى 5-أ-احسب Aمساحةحیزالمستوىالمحصوربینمنحنىالدالة gومحورالأفاصیل 1 حیث x و x 1 والمستقیمیناللذینمعادلتاهماعلىالتوالي lim ب-احسب الجزءالثالث unالمعرفةبمایلي نعتبرالمتتالیةالعددیة u g u n IN u n n 1 1 n IN 1un e بینأن-1 unتزایدیة 2-بینأن n متقاربةواحسبun 3-استنتجأن n u lim وااللهوليالتوفیق ملاحظةیراعىفيالتصحیحسلامةالتعبیروحسنالتقدیم حظسعیدللجمیع

تصحیحالامتحانالتجریبيالموحد 2007 ثانویةدمناتالتأهیلیة دمنات-أزیلال إعدادالأستاذسعیدالدحاني التمرینالأول t IR D تمثیلبارامتريللمستقیم-1 z t y t x t 1 1 1 2-لتحدیداحداثیاثالنقطة Bنحلالنظمة 2 0 1 1 1 x y z z t y t x t 1t 1t 1t 2 0 ومنه B200 وبالتالياحداثیاثنقطةالتقاطعهيt 1 أي 3-أ معادلةدیكارتیةللفلكة Sهي 2 2 2 2 x 1 y 1 z 1 7 x 2 y 2 z 2 2x 2y 2z 4 0 أي 3 7 بلدینا-3 3 3 1 1 1 1 1 1 2 d A P ومنهالمستوى Pیقطعالفلكة Sوفقدائرة مركزهاهوالمسقطالعموديللنقطة Aعلىالمستوى Pأيتقاطع المستقیمDوالمستوى Pأيالنقطة B r r 2 d 2 73 2 شعاعها 4 -معادلةدیكارتیةلمستوى Qموازيللمستوى Pتكتبعلى xy z d 0 شكل dA Q 2 یكافئS مماسللفلكةQ المستوى ولدینا 7 3 1 1 1 2 d d A Q 7 3 1 d 1d 21 1d 21 أو1d 21 d 1 21 أو d 1 21 ومنهمعادلتيالمستویینالموازیینللمستوى Pوالمماسینللفلكة xy z 1 21 0 هماS xy z 1 21 0 و التمرینالثاني Pz z 3 223iz 2 415iz 161i لدینا 2 2 22 3 2 41 5 2 161 لدینا-أ-1 3 2 P i i i 81 2 3 1 5 2 2 8 82 3 81 5 161 i i i i i i P جذرللحدودیةz 0 2 ومنه 2 بلدینا-1 2 P z z z az b z a 2z b 2az 2b 3 2 81 2 22 3 21 3 2 161 2 41 5 2 22 3 b i a i i b i b a i a i Pz z 2z 2 213iz 81i وبالتالي 1-جلدینا 0 2 21 3 81 0 P z z z 2 i z i 21 3 81 0 z 2 0 أوz 2 i z i 21 3 81 0 z 2 أوz 2 i z i لنحلالمعادلة b 2 ac 13i 2 81i 2i 1i 2 لدینا z1 13i1i 22i ومنه z2 13i 1i 4i و S 222i4i وبالتالي z 2 2i 8i وz0 z 2 8i لدینا-2 2 2 أي1 2 0 2 1 z z z إذن z 0و z1و z2حدودمتتابعةمنمتتالیةهندسیة i وبالتاليu1 z1 فإنu0 z0 وبماأن z z q 1 1 u16 u0 q 16 21i 16 22i 8 2 9 i 8 2 9 و C1 وB1 وA1 مرجحالنقطالمتزنةG النقطة-3 GA GB GC 0 یعني z A zG zB zG zC zG یكافئ 0 z G z A zB zC یكافئ z G 2i یكافئ التمرینالثالث I xe dx لدینا-1 x 1 1 نضع x x v x e u x v x e u x x 1 ومنه 1 1 I 1 xe 0 e dx x x أي 1 1 1 0 x x I xe e بالتالي e I 2 1 1 1لكل-2 I n x n e x dx لدیناnIN 1 نضع x n x n v x e u x nx v x e u x x 1 ومنه 1 1 1 I x e 0 n x e dx n x n x n أي e I nI n n 1 1

2-ب حسبالعلاقةالأخیرةلدینا e e e I I 1 2 21 1 2 2 1 أي e I 5 2 2 و e e e I I 1 5 32 1 3 3 2 أي e I 16 6 3 x x e dx x e x e dx جلدینا-2 x x x 2 4 2 4 2 1 3 1 3 2 1 2 1 3 2 x e dx 4 x e dx x x 3 41 5 42 16 26 2 4 3 2 e e e I I ألدینا-3 1 1 I I x x 1e dx n x n n 01سالبةعلىالمجال xx n x1e وبماأنالدالة x 1 0 فإن 1 Iتناقصیة n nIN ومنهالمتتالیة0 x n x e x dx 01موجبةعلىالمجالxx n e x الدالةn IN ولدینالكل إذن 0 1 I n 0 أي 0 x n e x dx 0 مصغورةبالعددI n ومنهالمتتالیة nIN بماأنالمتتالیة ب-3 n n IN I تناقصیةومصغورةبالعدد فإنهامتقاربة 1 01لدیناعلىالمجال ج-3 x e n IN لكل x n e x x ومنه n وبالتالي 1 1 x e dx x dx n x n أي 1 1 n I n بماأن 1 1 n I و n 1 1 lim xn lim 0 فإن n n I المسألة الجزءالأول لدینا-1 lim lim 1 ln 0 0 g x x x x w lim gx lim x 1 lnx و x x 1 ln lim 1 x x x x x 2-لكل xمن لدیناIR x x x g x 1 1 1 0 علىالمجالx 1 هيإشارةgx ومنهإشارة جدولتغیراتالدالة g x 0 1 gx - gx 2 3-لدینا 2قیمةدنیاللدالة gأيأنلكل xمن gx 2 IR gx 0 IR منx وبالتاليلكل الجزءالثاني lim lim 0 لدینا-1 ln 1 0 0 x x x x x f x e lim 0 ومنه f x f x إذنالدالة fمتصلةعلىالیمینفيالنقطة 0 لدینا ln 1 lim lim x x x x x f x e 2-أ لكل xمنالمجال0لدینا ln 1 ln 1 ln ln 1 ln ln 1 ln 1 1 x x x x x x x x x x x x x xe f x e e e e e وبالتالي ln 1 x x e x f x 2-بلدینا lim 0 lim lim ln 1 0 0 0 x x x x x e x f x x f x f ومنهالدالة fقابلةللاشتقاقعلىالیمینفيالنقطة 0 تأویلهندسي منحنىالدالة fیقبلنصفمماسأفقيفيالنقطة o أصلالمعلم lim 1 جلدینا-2 lim ln x x x x e x f x 2-دلدینا ln lim ln lim ln x xe x x f x x x x x x x x e x x e x x x x x x ln 1 lim ln 1 lim ln ln نضع x x t ln x t0 لدینا ومنه 1 1 lim ln lim t e x f x x t x t استنتاج ln ln lim lim x x f x x f x x x x منحنىالدالة fیقبلفرعاشلجمیافياتجاهالمستقیمذيالمعادلة y x
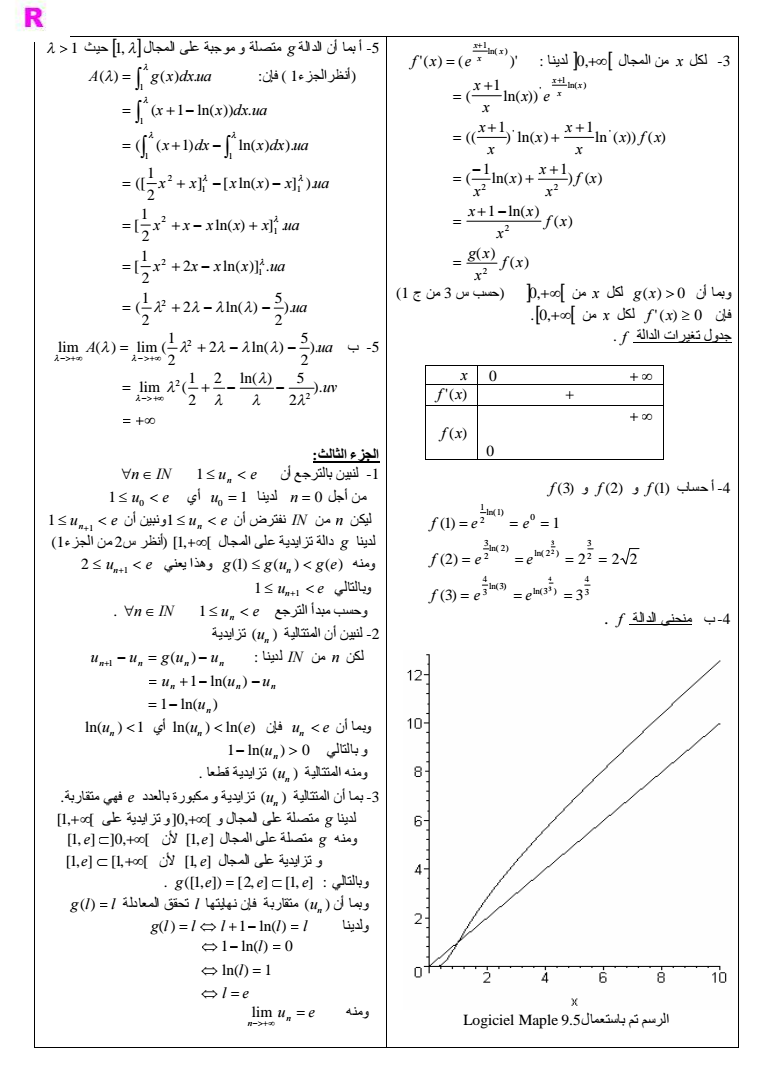
لدینا0منالمجالx لكل-3 ln 1 x x x f x e 1 ln 1 ln 1 ln 1 ln 1 ln 1 2 2 2 2 ln 1 f x x g x f x x x x f x x x x x x f x x x x x x x e x x x x x 1 منج3 حسبس 0منx لكلgx 0 وبماأن 0منx لكلf x 0 فإن جدولتغیراتالدالة f x 0 f x f x f 3 وf 2 وf 1 أحساب-4 3 4 ln3 ln3 3 4 2 3 ln 2 ln 2 2 3 ln1 2 1 3 3 2 2 2 2 1 1 3 4 2 3 f e e f e e f e e f بمنحنىالدالة-4 Logiciel Maple 95الرسمتمباستعمال 1 حیث1متصلةوموجبةعلىالمجالg أبماأنالدالة-5 A gxdxua فإن 1أنظرالجزء 1 ua x x x x ua x x x x x ua x x x x x ua x dx x dx ua x x dx ua 2 5 2 ln 2 1 2 ln 2 1 ln 2 1 ln 2 1 1 ln 1 ln 2 1 2 1 2 1 1 2 1 1 1 A ua ب -5 2 5 2 ln 2 1 lim lim 2 uv 2 2 ln 5 2 1 lim 2 2 الجزءالثالث n IN 1un e لنبینبالترجعأن-1 1u0 e أيu0 1 لدیناn 0 منأجل 1un1 e ونبینأن1un e نفترضأنIN منn لیكن 1منالجزء2أنظرس 1 دالةتزایدیةعلىالمجالg لدینا 2 un1 e وهذایعنيg1 gun ge ومنه 1un1 e وبالتالي n IN 1un e وحسبمبدأالترجع unتزایدیة 2-لنبینأنالمتتالیة un1 un gun un لكن nمن INلدینا 1 ln 1 ln n n n n u u u u lnun 1 أيlnun lne فإنun e وبماأن 1lnun وبالتالي 0 unتزایدیةقطعا ومنهالمتتالیة unتزایدیةومكبورةبالعدد eفهيمتقاربة 3-بماأنالمتتالیة 1 وتزایدیةعلى0 متصلةعلىالمجالوg لدینا 1 e 0 لأن1e متصلةعلىالمجالg ومنه 1e 1 لأن1 e وتزایدیةعلىالمجال g1e 2 e 1 e وبالتالي gl l تحققالمعادلةl متقاربةفإننهایتهاun وبماأن gl l l 1lnl l ولدینا l e l l ln 1 1 ln 0 un e ومنه n lim

الأكاديمية الجهوية للتربية والتكوين بجهة الدار البيضاء الكبرى الثانوية التأهيلية الحسين بن علي الامتحان التجريبي الموحد أبريل2007 لمستوى السنة الثانية من سلك الباكلوريا في مادة الرياضيات الشعبة علوم تجريبية مدة الإنجاز 3ساعات المعامل 7 الحدودية C في نعتبر 1مرين 3 2 Pz z iz i z i 5 7 26 6 241 احسب ثم P i 4 احسب - 1 2 ن1 1 3 i حيث C من b و a حدد - 2 ن15 P z 0 المعادلة حلول استنتج ثم z C P z z i z az b 4 Z B A Z i Z C i و 2 3 3 في المستوى العقدي المنسوب إلى معلم منعامد ممنظم مباشر نعتبر النقط B Aو C ألحاقها على التوالي 2 4 B C اكتب على الشكل المثلثي العدد A C z z z z 1 C 01 1 B 110 A10 1 النقط نعتبر Oi jk مباشر ممنظم متعامد معلم إلى المنسوب الفضاء في 2تمرين 1 احسب AB AC ثم اعط معادلة ديكارتية للمستوى 1 ABC - اعط تمثيلا بارمتري للمستقيم المار من النقطة D 213 العمودي على المستوى 05 ABCن ج- حدد H نقطة تقاطع و 05 ABCن 2 أ- اآتب معادلة دیكارتية للفلكة S التي أحد أقطارها 075 DHن ب- حدد تقاطع الفلكة S والمستوى 05 ABCن ج- اآتب معادلة دیكارتية للمستوى الموازي ل ABC قطعا والمماس للفلكة 075 Sن 3 تمرين1 3 احسب التكامل 1 1 ln e e I x dx x 1 2 باستعمال المكاملة بالأجزاء احسب التكامل 1 J x Arc xdx tan 1 3 احسب التكامل ln8 ln3 4 1 2 1 t t t e K dt e e 1 التالي التغيير مستعملا t 1 x e 2 مسألة f دالة عددیة معرفة على IR بما یلي ln 2 0 2 3 4 1 0 x x fx x x x x fx x e e x gt منحناها في معلم متعامد ممنظم Cf Oi j و في متصلة f الدالة أن بين - 1 lim احسب -ب ن05 x 0 0 x f x lim و x f x ن05 1 1 یلي بما IR على المعرفة h الدالة نعتبر 2 x hx x e ن1 x IR h x 0 أن وبين h الدالة تغيرات ادرس 3 - تحق من أن 2 2 3 1 4 1 0 2 x x x fx e e x e x xx 025 lt - استنتج أن f قابلة للإشتقاق في 0 على اليسار ثم ادرس قابلية اشتقاق f في 0 عن اليمين 1 4 0 و fx x x ln 1 0 gt أن بين -أ 4 x ن1 f x hxe x ب- اعط جدول تغيرات الدالة 05 fن بجوار 5 Cf 025 أ- ادرس الفرع اللانهائي للمنحنى 15ن Cf مع محور الأفاصيل 0ثم انشيء Cf في المجال ب- حدد تقاطع 6 ليكن g قصور الدالة f على المجال I e أ- بين أن g تقابل من المجال I نحو مجال J یتم تحدیده 05ن ب- انشيء منحنى الدالة g في نفس المعلم 05ن u حيث u0 0 و 7 n نعتبر المتتالية العددیة 1 1 n n n IN u g u أن بين -أ 3 n IN e u e n المتتالية أن بين -ب ن075 n ن05 قطعا تزایدیة u u متقاربة وحدد نهایتها 075 wwwmadarissfrن n ج- استنتج أن المتتالية
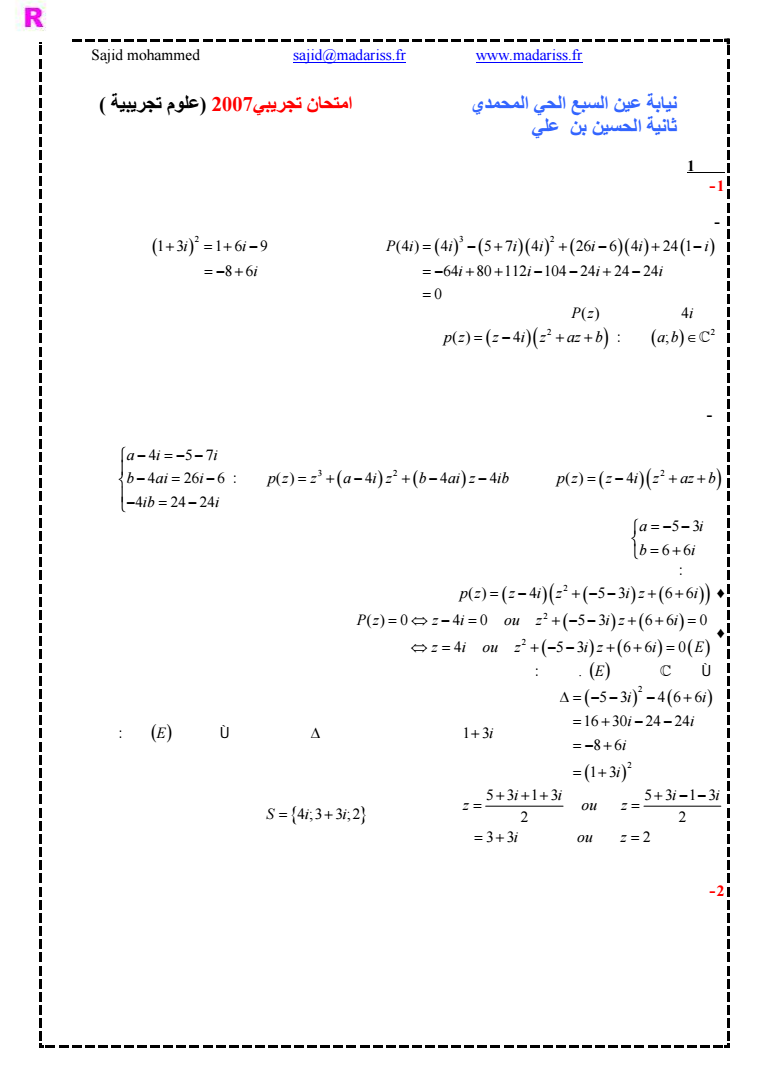
Sajid mohammed sajidmadarissfr wwwmadarissfr نيابة عين السبع الحي المحمدي امتحان تجریبي2007 علوم تجریبية ثانية الحسين بن علي تمرين1 -1 - 3 2 4 4 5 7 4 26 6 4 24 1 64 80 112 104 24 24 24 Pi i i i i i i i i ii إذن 4i جذر للحدودية Pz بالتاليى يوجد زوج 2 حيث a b 2 p 4 z z i z az b 2 13 16 9 8 6 i i i - 2 تكافئ p 4 z z i z az b 3 2 إذن p z z a i z b ai z ib 4 4 4 4 57 4 26 6 4 24 24 ai i b ai i ib i أي 5 3 6 6 a i b i خلاصة 2 p 4 5 3 6 6 z z i z iz i 2 2 0 4 0 5 3 6 6 0 4 5 3 6 6 0 P z z i ou z i z i z i ou z i z i E لنحل في المعادلة E لدينا 2 2 5 3 46 6 16 30 24 24 8 6 1 3 i i i i i i إذن 1 3i أحد الجذور المربعة للعدد منه فإن حلول المعادلة E هي 53 13 53 13 2 2 3 3 2 ii ii z ou z i ou z Si i 4 3 3 2 إذن -2

Sajid mohammed sajidmadarissfr wwwmadarissfr 4 2 33 2 4 2 1 3 4 213 10 4 12 2 6 10 1 2 4 A B C B zz i zz i i i i i i i i 1 تمرين2 -1 - AB211 لدينا JJJG AC110 JJJG أذن 110 1 1 2 01 1 2 1 1 AB AC JJJG JJJG AB AC 111 أي JJJG JJJG معادلة ديكارتية للمستوى ABC هي على الشكل xyzk 0 بما أن A ABC فإن 101 0 k أي k 0 ABC x y z 0 فإن منه - AB AC 111 بالمتجهة موجه المستقيم JJJG JJJG إذن D 213 من يمر 2 1 3 x t y tt z t - H 0 11 فإن ومنه t 2 أي 2 1 30 ttt حيث t البارامتر قيمة لنحدد -2 - MD MH 0 إذن الفلكة من نقطة M x yz لتكن JJJJG JJJJG 2 1 1 31 0 xx y y z z أي فإن ومنه 2 22 Sx y z x z 2 4 20 - 2 ليكن R مركز شعاع الفلكة S على التوالي لدينا DH للمستوى مماسة S الفلكة إذن d ABC R - ABC في النقطة H هذا المستوى هو المستوى المار من D الموازي ل ABC إذن معادلته هي آذلك تكتب على شكل xyzk 0 بما أن xyz 6 0 هي المستوى معادلة إذن k 6 أي 213 0 k فإن إليه تنتمي D 213 النقطة تمرين3 -1

Sajid mohammed sajidmadarissfr wwwmadarissfr 3 1 1 3 3 1 1 1 4 4 1 1 1 ln 1 1 ln ln 1 1 ln ln 4 4 1 1 4 4 1 2 e e e e e e I x dx x x dx x dx x x x x -2 2 2 2 1 1 2 2 0 0 1 2 0 1 1 tan 1 2 tan 1 1 1 4 1 tan 4 1 4 4 1 2 u x Arc x u x x vx x v x x x J x Arc x dx x dx x x Arc x -3

Sajid mohammed sajidmadarissfr wwwmadarissfr 2 ln8 ln3 3 2 2 3 2 3 2 3 2 1 12 ln8 3 ln 3 2 4 1 2 1 2 4 2 2 1 1 2 221 1 ln 2 1 2 1 ln 7 ln 5 2 1 7 ln 2 5 tt t t t t x e x e xdx e dt t x t x e K dt e e xdx x x dx x dx x x مسألة -1 - f 0 0 بما أن 0 0 lim lim ln 2 0 0 x x f x xx x f لأن 0 lim ln 0 x نهایة مرجعية فإن f متصلة في الصفر x x ب- lim lim ln 2 lim ln 2 x x x f x xx x x x 2 2 2 lim lim 2 3 4 1 lim 2 3 4 1 1 x x x x x x x x fx x e e xe e e -2 1 لدینا من x لكل x xx x إشارة هي h x إشارة h x e x e xe

Sajid mohammed sajidmadarissfr wwwmadarissfr x IR h x 0 إذن -3 - 2 2 2 2 2 2 2 2 3 4 1 0 2 3 34 1 2 3 14 1 3 1 4 1 2 x x xx x xx x x x x fx x e e x x x xe e e x xe e e x e e e x x - 2 بما أن 2 0 0 2 2 3 1 4 1 lim lim 2 1 1 lim 2 6 4 2 264 x x x x x x x x x fx e e e x xx e e e x x f g فإن f قابلة للاشتقاق على یسار الصفر و 0 0 لدینا 0 0 ln 2 lim lim lim ln 2 x x x f x xx x x x x إذن f غير قابلة للاشتقاق على یمين الصفر و منحناها یقبل نصف مما موازي لمحور الأراتيب على یمين الصفر موجه نحو الأراتيب السالبة -4 -
Sajid mohammed sajidmadarissfr wwwmadarissfr 0 ln 1 2 ln 1 x fx x x x e في تنعدم f x f 0 x xe f 0 0 x xe 2 2 2 0 2 2 2 3 4 4 1 4 1 1 4 4 xx x x x x x x x fx e e x e ex e ex e hx e إشارة f x على المجال 0 هي إشارة h x - -5 أ- ان بما lim lim ln 2 x x فإن منحنى الدالة f یقبل فرعا شلجميا في اتجاه محور الأرتيب بجوار f x x x ب- أي x fx x 0 0 ln 2 2 x e -6
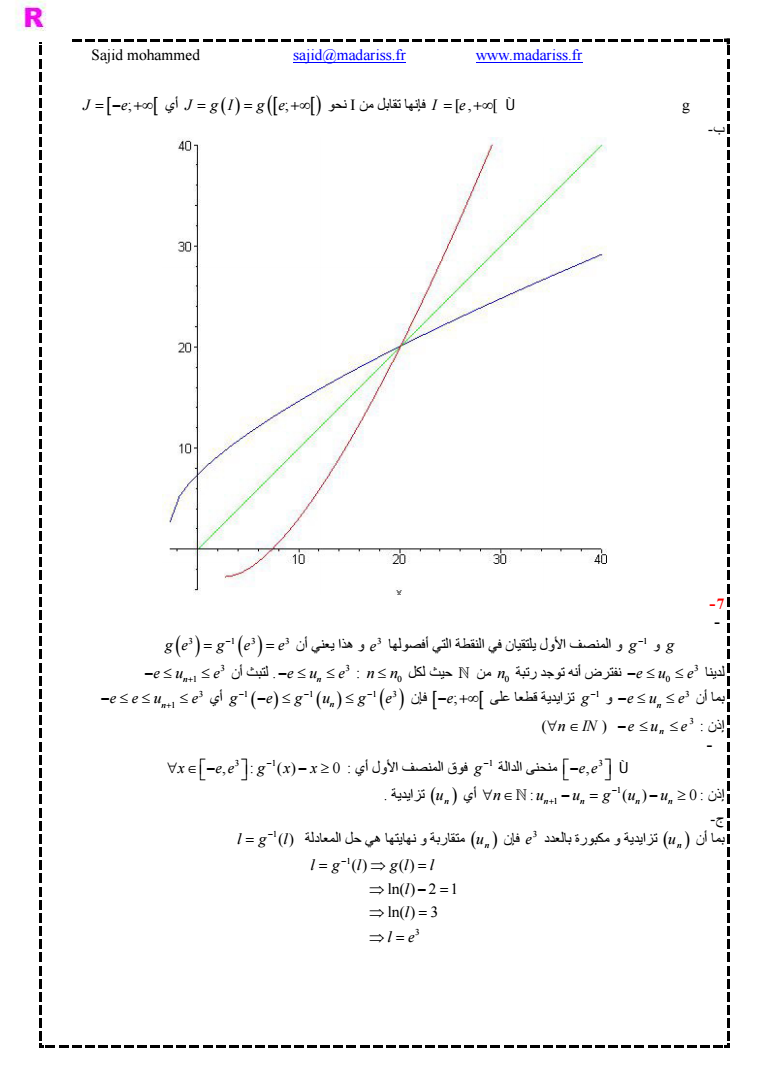
Sajid mohammed sajidmadarissfr wwwmadarissfr بما أن g متصلة تزايدية قطعا على المجال I e فإنها تقابل من I نحو J gI g e أي J e ب- -7 - 1 لاحظ أن g و و المنصف الأول یلتقيان في النقطة التي أفصولها g e و هذا یعني أن 3 3 13 3 ge g e e 3 لدینا 0 رتبة توجد أنه نفترض eu e 0 لكل حيث من n 0 n n 3 n أن لتبث eu e 3 n 1 eu e 3 بما أن n و eu e 1 g فإن e على قطعا تزایدیة 1 1 13 n g e gu ge أي 3 n 1 eeu e إذن 3 n IN e u e n - المجال على أنه لاحظ 3 e e الدالة منحنى 1 3 1 فوق المنصف الأول أي g x ee g x x 0 1 إذن 1 0 n n nn n u u gu u n أي تزایدیة u ج- u تزایدیة و مكبورة بالعدد n بما أن u متقاربة و نهایتها هي حل المعادلة e n فإن 3 1 lgl 1 3 ln 2 1 ln 3 l g l gl l l l l e

Sajid mohammed sajidmadarissfr wwwmadarissfr

الإمتحان التجريبي للسنة الثانية باآالوريا علوم تجريبية ثانوية الفتح نيابة الخميسات ذ عبد االله بن لختير دورة أبريل 2006 مادة الرياضيات مدة الإنجاز 3 ساعات Prof BENELKHATIR abouzakariyayahoofr 1 abouzakariyayahoofr يسمح باستعمال الآلة الحاسبة غير القابلة للبرمجة مسألة 07 نقط و نصف 1 f x x ln -- الجزء الأول نعتبر الدالة العددية f للمتغير الحقيقي x المعرفة بما يلي x G JG منحناها في معلم متعامد وممنظم Cf Oi j و ليكن Df ثم أحسب النهايتين 1- حدد lim x f x و lim x و اعط تأويلهما الهندسي 075 ن f x بجوار و 1ن Cf ثم أدرس الفرعين اللانهائيين ل x f x و 2 x f x lim- حدد النهايتين lim 3- أ- بين أن الدالة f قابلة للإشتقاق على Df و أن 2 1 f x xDfx x ن 025 025 ن Df ب- إستنتج رتابة الدالة f و أنشيء جدول تغيراتها على 3 2 2 يقطع محور الأفاصيل في نقطة وحيدة أفصولها ينتمي إلى المجال Cf ج- بين أن ن 05 quot 4- بين أن 3 2 f x xDfx x ثم أدرس تقعر Cf و حدد إحداثيتي نقطة إنعطافه 05 ن 075 ن 5 G JG- أرسم المماس T عند نقطة الإنعطاف و المنحنى Cf في المعلم Oi j 6- بين أن الدالة العددية F المعرفة على المجال 0 ب Fx x x x 1 ln دالة أصلية للدالة f على المجال 025 0 ن 7- إستنتج المساحة الهندسية للحيز D المحصور بين محور الأفاصيل و المنحنى Cf و المستقيمين اللذين ن 025 x e و x 1 معادلتهما -- الجزء الثاني لتكن g الدالة العددية المعرفة على بما يلي 1 0 0 x g x xe x g أن بين -أ -1 f x النهايتين إستنتج ثم x gx e 0 lim x g x و 0 lim x و اعط g x تأويلهما الهندسي 075 ن بجوار و 1 ن Cg ب- حدد طبيعة الفرعين اللانهائيين ل 2- أ- أدرس قابلية إشتقاق الدالة g على يسار x 0 0 و اعط التأويل الهندسي للنتيجة المحصل عليها 025 ن f x ثم إستنتج تغيرات الدالة g إنطلاقا من تغيرات الدالة 05 f ن بدلالة g x على ب- أحسب 3- أنشيء المنحنى Cg في معلم متعامد و ممنظم 05 ن

الإمتحان التجريبي للسنة الثانية باآالوريا علوم تجريبية ثانوية الفتح نيابة الخميسات ذ عبد االله بن لختير دورة أبريل 2006 مادة الرياضيات مدة الإنجاز 3 ساعات Prof BENELKHATIR abouzakariyayahoofr 2 abouzakariyayahoofr التمرين الأول نقطتين و نصف العدديتين المتتاليتين نعتبر n n 0 u و n n 0 v بحيث 3 1 n n u e u un ln و n n من n لكل v u متتالية هندسية و اعط أساسها و حدها الأول 075 ن 1 n n 0 v- بين أن 2 n- عبر عن الحد العام v n بدلالة n لكل n من ثم إستنتج lim n v ن 05 من n لكل -3 Pn n uu u 01 1 و S vv v n n 01 1 نضع n ثم إستنتج S lim n بدلالة n لكل n من n أ- عبر عن S ن 05 S n n ثم إستنتج n lim بدلالة Pn ب- عبر عن P ن 075 التمرين الثاني 05 نقط يحتوي صندوق على أربع آرات حمراء و آرتين سوداوين لا يمكن التمييز بينها باللمس 1- نسحب عشوائيا بالتتابع و بدون إحلال آرتين من الصندوق أحسب إحتمال آل حدث من الأحداث التالية quot سحبت آرة واحدة سوداء بالضبط quot A1 quot لم تسحب أية آرة سوداء quot و A0 quot الكرتين المسحوبتين سوداوين quot 075 ن A2 و 2- بعد السحب الأول بقيت في الصندوق أربع آرات نجري سحبا ثانيا لكرتين بالتتابع و بدون إحلال و نعتبر الأحداث التالية quot لم تسحب أية آرة سوداء عند السحب الثاني quot B0 quot سحبت بالضبط آرة واحدة سوداء عند السحب الثاني quot B1 quot الكرتين المسحوبتين عند السحب الثاني سوداوين quot B2 و التالية الإحتمالات أحسب -أ 0 A 0 و p B 1 A 0 و p B 2 A 0 ن1 p B0 إستنتج ثم p B ب- أحسب بنفس الطريقة الإحتمالين p B1 و 1 p B2 ن ج- إذا علمت أنه عند السحب الثاني حصلنا على آرة سوداء بالضبط فما هو إحتمال الحصول على آرة واحدة سوداء بالضبط عند السحب الأول 05 ن 3- نعتبر الحدث R quot لكي تسحب الكرتين السوداوين تم بالضبط إجراء السحب الأول والسحب الثاني quot بين أن 1 3 ن 075 p R 4- نسحب هذه المرة عشوائيا و في آن واحد ثلاث آرات من الصندوق و نعتبر المتغير العشوائي X الذي يربط آل سحبة ممكنة بعدد الكرات الحمراء المكونة لها حدد قانون إحتمال المتغير العشوائي X ثم أحسب الأمل الرياضي 1 E X ن

الإمتحان التجريبي للسنة الثانية باآالوريا علوم تجريبية ثانوية الفتح نيابة الخميسات ذ عبد االله بن لختير دورة أبريل 2006 مادة الرياضيات مدة الإنجاز 3 ساعات Prof BENELKHATIR abouzakariyayahoofr 3 abouzakariyayahoofr التمرين الثالث نقطة و نصف نعتبر النقطة 211 و المستوى G JG JG في الفضاء منسوب إلى معلم متعامد ممنظم Oi jk x yz 2 3 10 معادلته الذي 1- أآتب معادلة ديكارتية للفلكة S التي مرآزها و شعاعها 05 r 3 ن 2- أحسب d ثم إستنتج أن S دائرة C يتم تحديد مرآزها H و شعاعها 1 R ن التمرين الرابع ثلاث نقط و نصف الحدودية المجموعة في نعتبر 3 2 P z z iz i z i 2 3 41 3 8 1- بين أن المعادلة P z 0 تقبل حلا تخيليا صرفا z 0 ينبغي تحديده 025 ن 2 2- تحقق من أن 0 z Pz z z z z 23 4 العددين المجموعة في أوجد ثم 1 و z 2 المعادلة حلي z 2 z z 23 4 0 حيث 2 ن 05 Im 0 z 125 z z 2 0 و z z 1 0 و z 2 و z 1 و z 0 التالية العقدية الأعداد المثلثي الشكل على أآتب -3 4 G G- المستوى العقدي منسوب إلى معلم متعامد و ممنظم Ouv أنشيءالنقط A 0 و z B 1 و z الرباعي أن بين C z 2 ن 15 معين OABC ثم

ثانوية الفتح نيابة الخميسات تصحيح الإمتحان التجريبي لدورة أبريل 2006 2 ع ت 2 01 ع ت 02 Prof BENELKHATIR 1 مسألة الجزء الأول 1 f x x ln x 1- لدينا 0 و x 0 f xD x x 0 Df إذن - نهايتي f عند و 0 لدينا 1 lim lim lim ln x x x x f x x و 0 0 1 lim lim 1 ln x x f x xx x 0 وبما أن lim 1 ln 1 x x x و 0 1 lim x x 0 فإن lim x f x يقبل مقاربا رأسيا معادلته Cf x 0 نستنتج أن أي Oy لدينا -2 1 lim 0 x x lim lim ln إذن x x fx x 2 و 1 ln lim lim x x f x x x x x 2 و بما أن 1 ln lim lim 0 x x x x x فإن lim 0 x f x x يقبل بجوار و فرعين Cf و هذا يعني أن شلجميين إتجاههما Ox 3- أ- بما أن الدالة f مجموع دالتين قابلتين للإشتقاق على و لدينا إذن فهي قابلة للإشتقاق على 1 x ln fx x x 2 2 1 1 1 x x x x لدينا -ب x sg f x sg x 1 إذن الدالة f تزايدية قطعا على المجال 1 و تناقصية قطعا على المجالين 01 و 0 و جدول تغيراتها يكون على الشكل التالي x 0 1 - - 0 f x 1 f ج- من خلال جدول تغيرات الدالة f نستنتج أن x fx 1 إذن المعادلة E fx 0 لا تقبل حلا في المجال 0 و الدالة f تناقصية قطعا على المجال f و إذن المعادلة E fx 0 تقبل حلا وحيدا من المجال 0 و بما أن 1 ln 4 2 04 2 f e 2 27 2 ln 3 27 8 0 4 23 8 f e 3 2 فحسب مبرهنة القيم الوسيطية لدينا 2 يقطع Ox في نقطة وحيدة أفصولها Cf وبالتالي f دالة جذرية فإنها قابلة للإشتقاق على 4- بما أن مجموعة تعريفها و لدينا quot x fx f x 2 2 2 2 4 3 1 1 2 2 2 x x x x x x x x x x x إذن quot x 2 sg f x sg x x
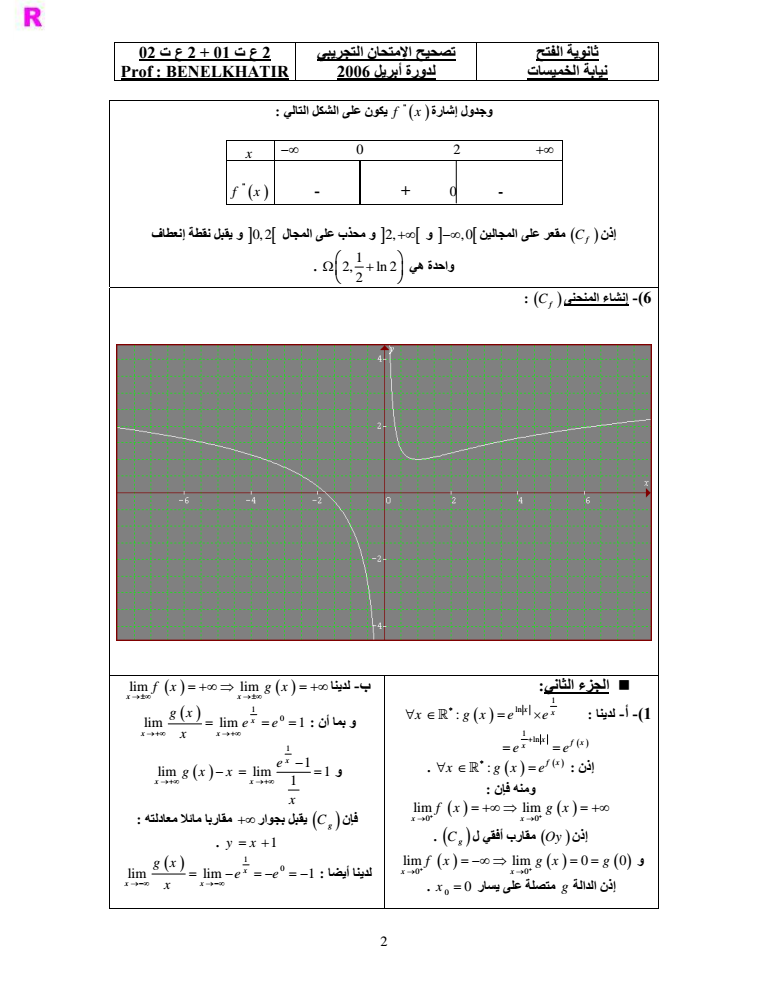
ثانوية الفتح نيابة الخميسات تصحيح الإمتحان التجريبي لدورة أبريل 2006 2 ع ت 2 01 ع ت 02 Prof BENELKHATIR 2 f x يكون على الشكل التالي quot وجدول إشارة x 0 2 - 0 - quot f x مقعر 0 و 2 و محذب على المجال 0 2 و يقبل نقطة إنعطاف Cf على المجالين إذن هي واحدة 1 2 ln 2 2 6- إنشاء المنحنى Cf الجزء الثاني 1 1- أ- لدينا ln x x x gx e e 1 ln x f x x e e إذن f x x gx e ومنه فإن 0 0 lim lim x x f x gx Cg إذن Oy مقارب أفقي ل و 0 0 lim lim 0 0 x x f x gx g 0 x 0 إذن الدالة g متصلة على يسار lim lim لدينا -ب x x f x gx 1 و بما أن 0 lim lim 1 x x x g x e e x و 1 1 lim lim 1 1 x x x e gx x x يقبل بجوار مقاربا مائلا معادلته Cg فإن y x 1 1 لدينا أيضا 0 lim lim 1 x x x g x e e x
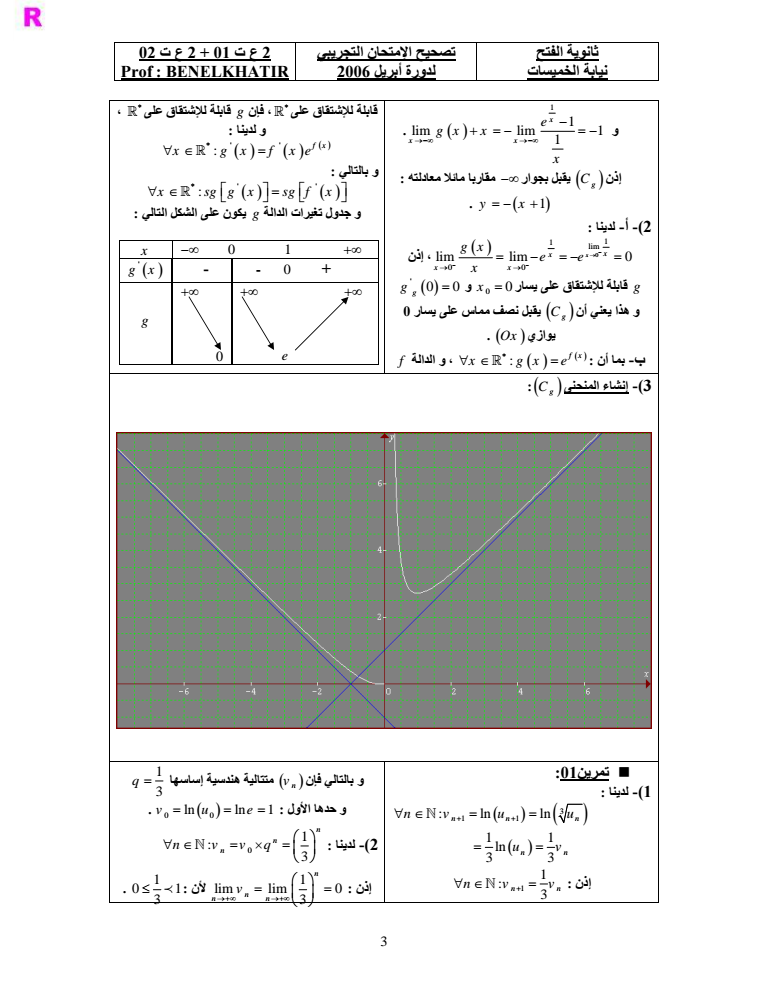
ثانوية الفتح نيابة الخميسات تصحيح الإمتحان التجريبي لدورة أبريل 2006 2 ع ت 2 01 ع ت 02 Prof BENELKHATIR 3 و 1 1 lim lim 1 1 x x x e gx x x يقبل بجوار مقاربا مائلا معادلته Cg إذن y x 1 2- أ- لدينا 1 1 lim 0 0 lim lim 0 x x x x x g x e e x إذن يسار على للإشتقاق قابلة g 0 و x 0 0 0 g g يقبل نصف مماس على يسار Cg 0 و هذا يعني أن يوازي Ox أن بما -ب f x f الدالة و x gx e فإن g قابلة للإشتقاق على قابلة للإشتقاق على و لدينا f x x g x f xe و بالتالي x sg g x sg f x و جدول تغيرات الدالة g يكون على الشكل التالي x 0 1 - - 0 g x e g 3- إنشاء المنحنى Cg تمرين01 1- لدينا 3 1 1 ln ln nn n nv u u 1 1 ln 3 3 n n u v 1 إذن 1 3 n n nv v v متتالية هندسية إساسها n و بالتالي فإن 1 3 q الأول حدها و 0 0 vue ln ln 1 0 لدينا -2 1 3 n n n n v vq إذن 1 lim lim 0 3 n n n n v لأن 1 0 1 3
ثانوية الفتح نيابة الخميسات تصحيح الإمتحان التجريبي لدورة أبريل 2006 2 ع ت 2 01 ع ت 02 Prof BENELKHATIR 4 3- أ- لدينا 1 1 3 1 1 3 n n n Sv إذن 3 1 1 2 3 n n S و بما أن 1 lim 0 3 n n فإن 3 lim 2 n n S 1 1 ب- لدينا 0 0 ln ln n n nk k k k nS u u إذن ln n n nS P n S هذه يعني أن n n Pe وبالتالي 3 lim 2 lim n n S n n P e e تمرين02 1- الصندوق يحتوي على 4 آرات حمراء و 2 سوداوين بما أننا في حالة تساوي الإحتمال لا يمكن التمييز بين الكرات فإن 2 0 4 0 2 6 card A A p A card A 0 إذن 43 2 65 5 P A و 1 1 1 4 2 1 2 6 card A 2 A A p A card A 1 إذن 241 8 6 5 15 P A و 2 2 2 2 6 21 1 6 5 15 A p A A A A A تجزيء للفضاء 012 لاحظ أن المثلوث أن و 012 pA pA pA 1 2- أ- ب- نحسب الإحتمالات الشرطية 0 A 0 و p B 1 A 0 و p B 2 A 0 p B A0 فإن الصندوق يحتوي على آرتين - إذا تحقق الحدث حمراوين و آرتين سوداوين إذن 2 2 0 2 4 2 1 12 6 A A p B A لدينا في هذه الحالة أيضا 1 1 2 2 1 2 4 2 8 2 12 3 A A A p B A 0 و 2 2 2 2 4 2 1 12 6 A A p B A 3 آرات A1 فإن الصندوق يحتوي على - إذا تحقق الحدث حمراء و آرة واحدة سوداء إذن 1 2 3 0 2 4 32 1 12 2 A A p B A و في هذه الحالة يكون لدينا 1 1 1 3 1 1 2 4 2 231 1 12 2 A A A p B A و 1 2 2 4 0 0 A p B A لا يمكن سحب آرتين سوداوين لأن الصندوق يحتوي على آرة واحدة سوداء 4 آرات A2 فإن الصندوق يحتوي على - إذا تحقق الحدث حمراء فقط إذن 2 0 1 A و p B 2 2 1 2 0 A A pB pB الآن نستنتج 0 p B2 و p B1 و p B نطبق صيغة الإحتمالات الكلية فنحصل على 21 8 1 1 1 5 6 15 2 15 p B 0 إذن 141 6 2 15 15 5 p B 1 و 22 8 1 1 0 5 3 15 2 15 p B 1 إذن 44 8 15 15 p B 2 و 21 8 1 0 0 5 6 15 15 p B 2 إذن 1 15 p B ولاحظ أنه في هذه الحالة لدينا pB pB pB 012 1 الشرطي الإحتمال نحسب -ج 1 B 1 p A 1 1 1 1 1 1 1 1 1 A B pA B p A pB p A pB pB إذن 1 1 8 1 15 2 1 8 2 15 B p A أن بمعنى R A BA B 0 21 1 لدينا -3 الحدث R مكون من سبيلين

ثانوية الفتح نيابة الخميسات تصحيح الإمتحان التجريبي لدورة أبريل 2006 2 ع ت 2 01 ع ت 02 Prof BENELKHATIR 5 إذن 21 8 1 1 5 6 15 2 3 p R 4- إذا سحبنا من الصندوق 3 آرات في آن واحد فكل سحبة ممكنة عبارة عن تأليفة ل 3 عناصر من بين 6 3 إذن 6 card C 20 و إذا آان X هو المتغير العشوائي الذي يربط آل سحبة ممكنة بعدد الكرات الحمراء المكونة لها فإن لدينا و X 1 23 1 2 4 2 1 1 20 5 C C p X و 2 1 4 2 3 2 20 5 C C p X و 3 4 1 3 20 5 p X أنشىء جدولا تحدد فيه C قانون إحتمال المتغير العشوائي X إذن 131 123 2 555 E X تمرين03 211 مرآزها التيS للفلكة ديكارتية معادلة -1 و شعاعهاr 3 هي 2 22 2 x yz 2 1 13 أي 2 22 xyz x yz 4 2 2 30 2- لدينا 2 2 2 2 2 1 3 1 10 12 3 d P أي 9 9 14 14 d P و بما أن 3 1 14 d Pr فإن إذن S P دائرة C شعاعها R يحقق 2 2 dd P حيث R r d لدينا 81 45 5 9 3 14 14 14 R مرآز الدائرة C هي النقطة H نقطة تقاطع المستقيم D المار من و العمودي على المستوى P لدينا 2 1 2 1 3 x t D y tt z t 2 2 1 2 3 1 3 10 0 t tt و أي 14 9 0 t يكافيء 9 14 t نعوض في تمثيل D فنجد إحداثيات النقطة H 37 16 13 14 7 14 H تمرين04 إذن حيث z i نضع -1 3 2 Pi i i i 2 3 أي 41 3 8 ii i 3 2 Pi i 23 2 2 4 8 ومنه 3 2 2 0 2 4 80 P i P i 0 2 إذن و بالتالي فالمعادلة P z 0 تقبل حلا تخيليا صرفا هو 0 z i 2 2 2 z z 23 4 0- نحل في المجموعة المعادلة من الدرجة الثانية هو المختصر المميز 2 2 3 41 i إذن حلي المعادلة هما 1 Im 0 z 2 z i 2 3 و z i 3 3- لدينا 0 2 2 z 1 و 3 1 2 2 22 6 z i و 10 2 1 2 6 zz z z و 2 0 1 3 3 3 23 2 2 3 zz i i إذن 2 0 2 3 3 z z 4- لدينا z z z aff AB aff OC 10 2 0 JJJG JJJG هذا يعني أن الرباعي JJJG JJJG OABC إذن OC AB متوازي أضلاع

ثانوية الفتح نيابة الخميسات تصحيح الإمتحان التجريبي لدورة أبريل 2006 2 ع ت 2 01 ع ت 02 Prof BENELKHATIR 6 arg 2 أن بما و C A B z z OB AC z JJJG JJJJG و 2 0 1 3 3 6 C A B z z zz z z فإن 2 2 OB AC JJJG JJJJG إذن قطرا متوازي الأضلاع OABC متعامدان و بالتالي فهو معين abouzakariyayahoofr و ما نيل المطالب بالتمني و لكن تأخذ الدنيا غلابا abouzakariyayahoofr

الأآاديمية الجهوية للتربية والتكوين الإمتحان التجريبي الموحد أبريل 2006 مدة الإنحاز 3 ساعات جهة الدارالبيضاء الكبرى المادة الرياضيات المستوى الثانية من سلك البكالوريا المعامل 7 الثانوية التأهيلية الحسين بن علي الشعبة العلوم التحريبية يسمح باستعمال الآلة الحاسبة غير القابلة للبرمجة التمرين الأول ثلاث نقط النقط G G G نعتبر في الفضاء المنسوب إلى معلم متعامد ممنظم مباشر O i jk 2 21 C001 B 100 A110 1 JJJG JJJG أ حدد إحداثيات المتجهة AB AC ب تحقق أن x 2 y z10 هي معادلة ديكارتية للمستوىABC ج إعط تمثيلا بارامتريا للمستقيمD المار من و العمودي على المستوى ABC 2 أ حدد معادلة ديكارتية للفلكةS التي مرآزها و المماسة للمستوى ABC ب حدد إحداثيات H نقطة تماس الفلكةS و المستوى ABC التمرين الثاني ثلاث نقط ونصف لتكن n n u بمايلي المعرفة العددية المتتالية u 0 0 3 3 n1 n 1 u 1u 8 أن بالترجع بين 1 n n 0u 1 u ثم استنتج أنها متقاربة لاحظ أن 2 n أدرس رتابة 3 3 n n 8u 2 u 3 نضع 3 n n n v u1 v 1 متتالية هندسية أساسها n أ بين أن 2 n n بدلالة n و احسب v un ثم n ب أآتب lim u 3 33 3 نضع 4 أحسب Suuu u n 0 1 2 n1 quot Sn n بدلالة التمرين الثالث أربع نقط المعادلة المجموعة في نعتير 2 E z 1 3i 3z 8 0 أحسب أ 1 2 3 i 3 ب حل في المعادلة E ج أآتب حلي المعادلةE على الشكل المثلثي wwwmadarissfr

النقطتين A و2 G G B نعتبر في المستوى العقدي المنسوب إلى معلم متعامد ممنظم مباشر Ouv لحقاهما على التوالي A z 1 i3 B و z 2 2i 3 B A أ تحقق أن B z z 3i z و استنتج طبيعة المثلث OAB ب حدد العدد العقدي zC لحق النقطة C بحيث يكون الرباعي OBAC مستطيلا مسألة تسع نقط و نصف x 0 بمايلي على المعرفة f العددية الدالة نعتبر 2x x fx lne e 1 fx xlnx 1 x 0 G حيث G G i 2cm و ليكنC ا لمنحنى الممثل للدالة f في معلم متعامد ممنظم O i j في متصلة f أن تحقق 1 0 x 0 2 أ تحقق أن x 0 2x x x x 2x x fx lne e 1 e 1 e x x e e x 0 fx lnx 1 x x x 0 وأن 0 f 0 1 ب استنتج أن f قابلة للإشتقاق في أحسب 3 x lim fx x و lim fx x و fx lim ثم حدد الفروع اللانهائية للمنحنى x C 4 أ بين أن x 0 x x 2x x e 2e 1 f x e e1 x 0 x lnx 1 x 1 f x 2 xlnx 1 ب استنتج أن f تزايدية قطعا على آل من المجالين ln 20 و 0 و تناقصية قطعا ln 2 على 5 أنشئ المنحنىC نقبل أن C يقبل نقطة انعطاف أفصولها أصغر من 1 6 أ أحسب التكامل 1 2 x dx 1 x ب استنتج حجم المجسم المولد بدوران C حول محور الأفاصيل دورة آاملة على المجال 01 استعمل المكاملة بالأجزاء I ln 20 المجال على f الدالة قصور h ليكن 7 أ بين أن h تقابل من I نحو مجال J يجب تحديده حدد ب 1 h x wwwmadarissfr J من x لكل


Sajid mohammed sajidmadarissfr wwwmadarissfr التمرين الأول AB 2 10 -أ 1 JJJG AC 1 11 و JJJG إذن 1 11 0 1 2 10 1211 AB AC JJJG JJJG أي AB AC 1 2 1 JJJG JJJG AB AC أن بما -ب JJJG JJJG أن بما و ABC x y z e 2 0 فإن ABC المستوى على منظمية متجهة ABC للمستوى دیكارتية معادلة x yz 2 10 فإن منه و e 1 أي 1 0 e فإن C ABC متجهة موجهة للمستقيم D إذن تمثيل JJJG JJJG منظمية على المستوى ABC فإن JJJG JJJG AB AC ج- بما أن AB AC بارامتري للمستقيم D هو 2 22 1 x t D y tt z t 2أ- شعاع الفلكة S هو 2 2 2 2 22 11 12 1 2 6 6 R d ABC إذن 2 2 2 2 6 2 2 1 6 Sx y z أي 2 22 25 442 0 3 Sx y z x y z التمرين الثاني 0 1 نضع 1 Pn u n لدینا 0 صحيحة عبارة P 0 أي 0 1 u نفرض أن P n عبارة صحيحة لكل عدد صحيح طبيعي أصغر من أو یساوي n لدینا حسب الفرضية السابقة 3 3 3 3 3 3 1 0 10 1 1 1 2 1 1 8 1 1 1 1 8 8 1 1 8 n n n n n n u u u u u u أي 1 0 1 n u 0 1 من n لكل إذن n u 2 لكل n من لدینا

Sajid mohammed sajidmadarissfr wwwmadarissfr 3 3 1 3 3 3 3 3 3 2 2 33 3 3 3 3 2 2 3 3 33 3 1 1 8 1 8 8 1 2 8 1 2 1 21 2 8 1 1 21 2 8 nn n n n n n n nn n n n n n n nn n uu u u u u u u uu u u u u u u uu u إشارة n n 1 u u u u n n 1 0 من n لكل وبالتالي 3 un 1 فإن 0 1 un أن بما و 1 3 un إشارة هي متتالية تزایدیة n n u أي متتالية تزایدیة و مكبورة فهي إذن متقاربة n u خلاصة n 3أ- لكل n من 3 1 1 3 3 3 3 3 1 1 1 1 8 1 1 1 2 1 1 2 2 1 2 n n n n n n v u u u u v 1 متتالية هندسية أساسها n n v إذن 2 ب- لكل n من 1 2 1 1 2 1 2 n n n n v v العلاقة من 3 1 n n أن نستنتج n Nv u 3 3 1 1 1 2 n n n u v 3 1 lim lim 1 1 2 n n n n u لأن 1 lim 0 2 n n

Sajid mohammed sajidmadarissfr wwwmadarissfr 4 3 3 3 3 012 1 012 1 012 1 1 1 1 1 1 1 2 1 1 2 1 2 1 2 n n n n n Su u u u vvv v n vvv v n v n التمرين الثالث 1 أ- 2 3 3 9633663 ii i ب- 2 1 3 3 32 1 6 3 27 32 663 i i i إذن 3 3 i هو أحد الجذور المربعة للعدد العقدي 1 13 3 3 3 223 2 i i z i 1 13 3 3 3 1 3 2 i i z i arg 2 1 z1 4 -ج 3 z 1 4 إذن 3 z 2 z 2 2 2 arg 2 3 z 1 إذن 2 2 3 z 2 أ- 1 3 223 1 3 3 3 1 3 3 31 3 4 333 33 4 3 B A B i i z z z i i i i i i i i

Sajid mohammed sajidmadarissfr wwwmadarissfr B A بما أن B z z z arg 2 2 فأن 3 عدد تخيلي صرف B A B z z z و نعلم أن arg 2 B A B z z BO BA z أي OAB مثلث قائم الزاویة في الرأس JJJG JJJG B ب- OAB مثلث قائم الزاویة في B إذن آي یكون OBAC مستطيل یكفي أن یكون OBAC متوازي الأضلاع أي OC BA JJJG JJJG BA3 3 أن بما و JJJG 3 3 إذن C3 3 فإن Cz i مسألة f 0 0 ln0 1 0 لدینا 1 و بما أن 2 0 0 lim lim ln 1 ln1 1 1 x x x x fx e e f فإن الدالة f متصلة في 0 2أ- الجواب في متناول الجميع ب- 2 2 0 0 lim ln 1 1 lim 1 g x x x x x x x x f x f x e e e e ee x 2 لأن 2 0 0 ln 1 ln 1 0 lim lim 1 x x g x x x h e e h f ee h و 1 lim 1 x x e x 0 lim ln1 lim 1 d x x f x f x x x أن بما 0 01 g d و 0 في للإشتقاق قابلة f الدالة فإن f f f 0 1 3 2 lim lim ln 1 0 x x x x fx e e lim lim ln 1 x x fx x x

Sajid mohammed sajidmadarissfr wwwmadarissfr ln 1 lim lim ln 1 1 lim 1 x x x fx x x x x x x x لأن ln 1 ln lim lim 0 x h 1 x h x h و 1 lim lim 1 x x x x x x x خلاصة بما أن lim 0 f x فإن المستقيم y 0 مقارب أفقي لمنحنى الدالة f بجوار lim 0 بما أن x f x فإن منحنى الدالة f یقبل فرعا شلجميا في اتجاه محر الأفاصيل x 4أ- - لكل x 0 لدینا 2 2 2 2 2 2 1 2 1 2 1 1 x x x x x x x x x x x x e e f x e e e e e e e e e e e و x لاحظ أن الصيغ 2 1 x x إشارة هي 0 المجال على f x إشارة إذن 0 على قطعا موجبة e e 2 1 العدد x 2 1 e x x ln 2 عند تنعدم e - لكل x 0 لدینا ln 1 1 2 ln 1 x x x f x x x بالتالي و ln 1 0 x أي x 1 1 x 0 لكل أن لاحظ ln 1 0 1 x x x 0 من x لكل f x 0 أي ب-
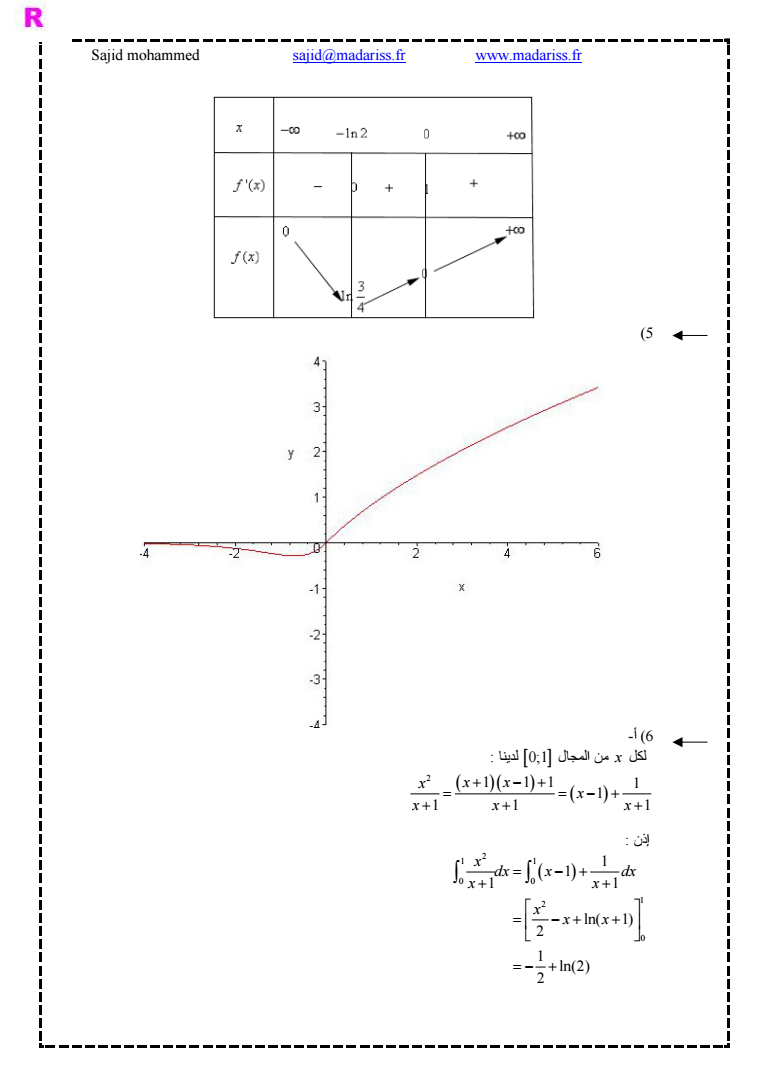
Sajid mohammed sajidmadarissfr wwwmadarissfr 5 6 أ- لكل x من المجال 01 لدینا 2 1 11 1 1 11 1 x x x x x x x إذن 2 1 1 0 0 1 2 1 1 1 1 ln 1 2 1 ln2 2 x dx x dx x x x x x
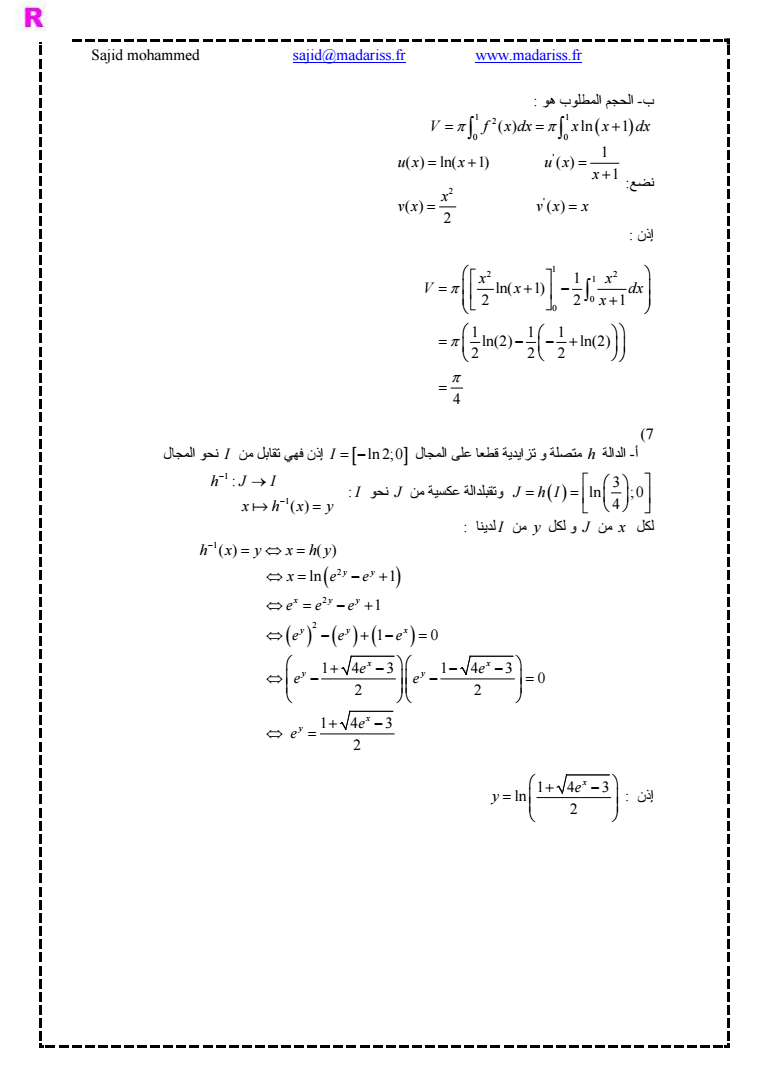
Sajid mohammed sajidmadarissfr wwwmadarissfr ب- الحجم المطلوب هو 1 1 2 0 0 V f x dx x x dx ln 1 نضع 2 1 ln 1 1 2 ux x u x x x vx v x x إذن 1 2 2 1 1 ln 1 2 21 1 11 ln2 ln2 2 22 4 x x V x dx x 7 أ- الدالة h متصلة و تزایدیة قطعا على المجال I ln 20 إذن فهي تقابل من I نحو المجال 3 ln 0 4 J hI I نحو J من عكسية وتقبلدالة 1 1 hJ I x hx y 6 لكل x من J و لكل y من I لدینا 1 2 2 2 ln 1 1 1 0 14 3 14 3 0 2 2 14 3 2 y y x yy yy x x x y y x y h x y x hy x ee ee e ee e e e e e e e إذن 14 3 ln 2 x e y

wwwmadarissfr 1 نيابة فاس الجديد دار دبييغ امتحان تجريبي علوم تجريبية التمرين الأول 75 ن نعتبر الدالة العددية f المعرفة على بما يلي 3 2 1 1 0 3 ln 0 x x fx x x fx e x x 1 بين أن f متصلة في الصفر 05 ن lim احسب 2 x f x lim و x f x 1 ن أن أثبت -أ 3 2 0 ln 1 x ن 05 x f x x xe ب- استنتج أن Cf منحنى الدالة f يقبل المستقيم الذي معادلته y x آمقارب مائل بجوار 025 ن ج- حدد موقع Cf بالنسبة لمقاربه عندما يكون 05 x 0 ن بجوار 05 ن Cf د- حدد الفرع اللانهائي للمنحنى 4 ادرس قابلية اشتقاق f في الصفر على اليمين و على اليسار ثم اعط تأويلا هندسيا للنتيجة 15 ن 3 تذآير 3 2 3 1 1 1 a a a a 0 و ln1 lim 1 h h h 6 5 لتكن f الدالة المشتقة الأولى للدالة f بين أن 075 ن 2 3 2 1 1 0 1 3 1 2 1 0 1 x x x fx x xe x fx x e 6 ضع جدول تغيرات الدالة 05 f ن أنشئ7 Cf Oi j ممنظم متعامد معلم في G G ن 1 x 6 1 x على المجال 0 التي تنعدم في الصفر 05 ن 8 3 أ- حدد دالة أصلية للدالة ب- احسب التكامل 7 3 و Cf المستقيمات ذات ثم استنتج مساحة الحيز المحصور بين المنحنى I 1 1 x dx و x 7 و x 0 المعادلات 3 y سؤال إضافي x التمرين الثاني 3 ن Oi jk مباشر ممنظم متعامد لمعلم منسوب الفضاء في G G G و B 1 3 2 و A5 12 النقط نعتبر C 2 12 AB AC احسب 1 JJJG JJJG ن 075 ABC المثلث مساحة استنتج ثم sin AB AC احسب 2 JJJG JJJG ن 05

wwwmadarissfr 2 3 احسب مسافة النقطة B عن المستقيم 075 AC ن 4 حدد تقاطع المستوى ABC و الفلكة التي أحد أقطارها 1 AB ن التمرين الثالث 35 ن يحتوي آيس على 3 آرات بيضاء و 4 آرات سوداء و 3 آرات حمراء نسحب عشوائيا و تآنيا 3 آرات من الكيس نفترض أن جميع الكرات لا يمكن التمييز بينها باللمس 1 حدد آون الإمكانيات و احسب 05 card ن 2أ- احسب احتمال الحدثين 075 ن A quot الحصول على 3 آرات من نفس اللون quot B quotالحصول على الأقل على آرة حمراء quot ب- هل الحدثان A و B مستقلان علل جوابك 05 ن 3 ليكن X المتغير العشوائي الذي يساوي عدد الكرات الحمراء المسحوبة حدد قانون احتمال 125 X ن 4 نعيد التجربة السابقة 5 مرات احسب احتمال الحصول على آرات من نفس اللون مرتين بالضبط 05 ن التمرين الرابع 3 ن المعادلة المجموعة في نعتبر 2 E z i zi 1 1 3 30 z يجب تحديده 05 ن 1 0 أ- بين أن المعادلة E تقبل حلا تخيليا صرفا ب- استنتج الحل الثاني للمعادلة 05 E ن 1 هي التوالي على ألحاقها Cو B و A النقط لتكن 2 A z i c 1 3 و z i B و z i z على الشكل المثلثي 075 ن z C و z B و A أ- اآتب ب- حدد قياسا للزاوية AB AC JJJG JJJG ن 05 ن 075 zi zi 13 1 يحيث z اللحق ذات M النقط مجموعة حدد 3 التمرين الخامس 3 ن المعرفة بما يلي n n u نعتبر المتتالية 1 21 2 n n n uu u 1 أن بين 1 n ن 05 n u 1 نضع 2 n n n vu 1 v ن 0 متتالية هندسية و حدد أساسها و حدها الأول n n v أ- بين ان ln نضع -ب n n nwv متتالية حسابية 05 ن n n w بين أن n ج- احسب lim n n w n v 1 ن

Sajid mohammed sajidmadarissfr wwwmadarissfr نيابة فاس الجديد دار دبييغ امتحان تجريبي علوم تجريبية التمرين الأول -1 و f00 2 0 0 0 0 lim lim ln 0 x x x x x fx e x 0 أي lim 0 x x f x f إذن f متصلة في 0 -2 3 3 3 2 lim lim 1 1 3 11 1 1 lim 3 x x x x fx x x x x x 2 lim lim ln x x x f x ex شكل محدد -3 أ- 2 2 2 2 0 ln ln 1 ln ln 1 ln 1 x x x x x x x fx e x e xe e xe x xe ب- بما أن 2 2 2 lim ln 1 lim ln 1 4 0 2 x x x x x xe e فإن المستقيم y x مقارب مائل لمنحنى الدالة f بجوا ر ج- لدينا x 0 لكل 2 ln 1 0 x لأن f x x xe 2 1 1 x فوق Cf إذن f x x أي x e المقارب المائل y x د- 3 3 2 1 1 1 1 1 lim lim x x 3 3 f x x x xx 3 lim lim 1 1 x x 3 x fx x إذن منحنى الدالة يقبل فرعا شلجميا في اتجاه المستقيم 3 x بجوار y -4 بما أن

Sajid mohammed sajidmadarissfr wwwmadarissfr 3 0 0 0 0 3 2 3 3 2 3 3 0 2 3 3 1 1 0 3 lim lim 1 1 3 lim 1 1 3 1 11 lim 3 1 11 lim 1 1 lim 3 1 11 x x x x x x x x x x x x x x fx f x x x x x x x x x x x x x x x x x فإن f قابلة للاشتقاق على يمين 0 و f منحنى الدالة f يقبل نصف مماس موازي لمحور الأفاصيل على يمين 0 0 d الصفر بما أن 2 0 0 0 0 2 2 2 0 0 ln lim lim ln ln 1 lim ln 1 lim 1 1 x x x x x x x x x x x x x x fx f e x x x e xe x x e xe x e فإن f قابلة للاشتقاق على يسار 0 و f منحنى الدالة f يقبل نصف مماس على يسار الصفر معامله الموجه هو 0 1 g 1 -5 1 1 3 2 3 2 3 1 1 1 3 3 1 1 1 3 1 1 1 3 1 x fx x x x لاحظ أنه لكل x 0 2 3 1 1 1 x أي 2 2 2 2 2 1 2 0 1 x x xx x xx x x x e x x fx e x e e xe e e xe x e x e
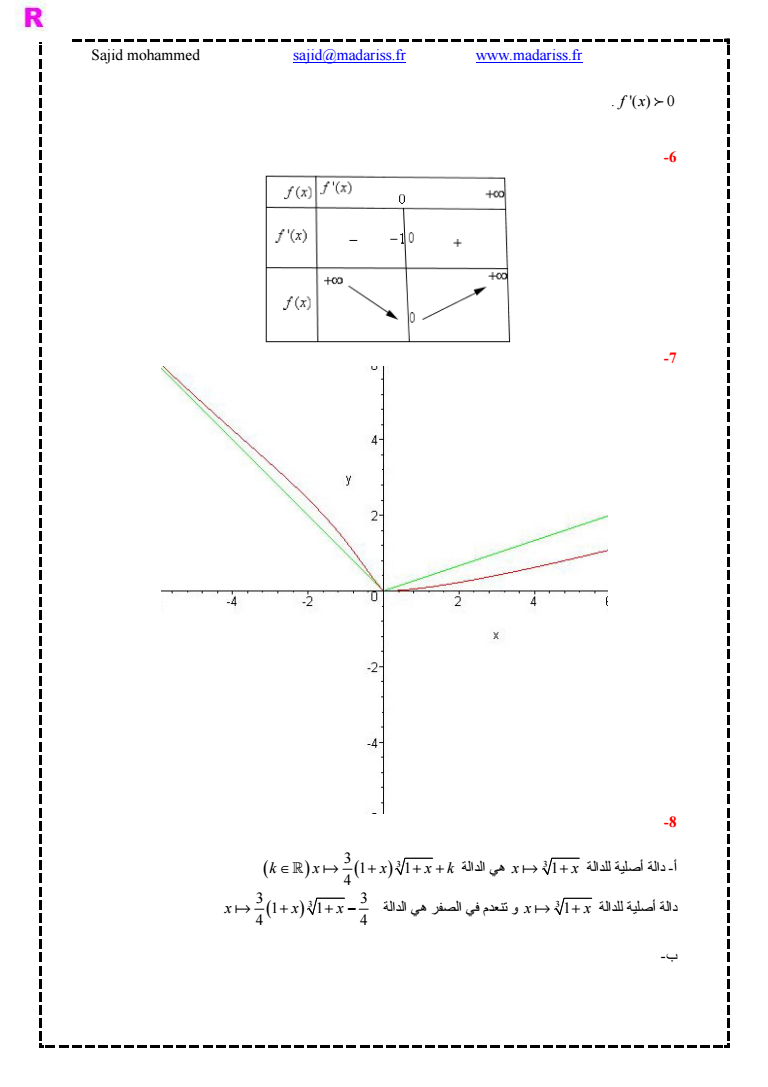
Sajid mohammed sajidmadarissfr wwwmadarissfr f x 0 -6 -7 -8 x 6 1 x هي الدالة 3 أ- دالة أصلية للدالة 3 3 1 1 4 k x x xk 6 x 6 1 x و تنعدم في الصفر هي الدالة 3 دالة أصلية للدالة 3 3 3 1 1 4 4 x xx 6 ب-

Sajid mohammed sajidmadarissfr wwwmadarissfr 7 3 7 3 1 1 3 3 1 1 4 4 17 4 I x dx x x x 7 7 3 7 3 3 1 1 1 1 17 4 x S f x dx x dx x dx التمرين الثاني 3 ن -1 AB 4 2 4 JJJG AC 700 و JJJG إذن 20 4 0 4 7 40 4 7 2 0 AB AC JJJG JJJG أي AB AC 028 14 JJJG JJJG مساحة المثلث ABC هي 22 2 1 2 1 0 28 14 2 1 784 196 2 7 5 S AB AC JJJG JJJG -2 sin 14 5 6 7 5 3 AB AC AB AC AB AC JJJG JJJG JJJG JJJG JJJG JJJG -3

Sajid mohammed sajidmadarissfr wwwmadarissfr 14 5 7 2 5 AB AC d B AC AC JJJG JJJG -4 بما AB ABC فإن منتصف القطعة AB أ ي مرآز الفلكة ينتمي إلى المستوى ABC إذن 0 2 d ABC و عليه فإن الفلكة تقطع المستوى وفق دائرة آبرى مرآزها و شعاعها AB 2 AB التمرين الثالث 35 ن -1 آون الامكانيات يتكون من تأليفات ل 3 آرات من بين 10 آرات 3 10 10 3 7 8 9 10 6 120 card C -2 أ- احتمال الحدث A 333 343 120 141 120 1 20 cardA P A card CCC احتمال الحدث B 3 7 1 120 85 120 C P B ب- A B quotالحصول على 3 آرات حمراء quot 3 3 1 120 120 C PA B P A B PA PB لأن مستقلين غير الحدثان -3

Sajid mohammed sajidmadarissfr wwwmadarissfr 3 7 1 2 3 7 2 1 3 7 3 3 0123 35 0 120 120 3 21 63 1 120 120 120 3 7 21 2 120 120 120 1 0 120 120 X C P x C C P x C C P x C P x -4 2 3 2 5 2 3 2 5 1 1 19 20 20 P C PA PA C التمرين الرابع 3 ن -1 أ- المعادلة E تقبل حلا تخيليا صرفا i يعني 2 تعني i i ii 1 1 3 30 2 تعني 13 3 1 0 i و 1 0 2 1 أي 13 30 0 z i إذن E تقبل حلا تخيليا صرف و هو ب- ليكن z1 الحل الثاني للمعادلة E لدينا 0 1 أي zz i 113 1 z i ii 113 1 3 -2 أ- 1 2 4 A z i 1 2 Bz i 1 3 2 3 Cz i ب- arg 2 arg 3 1 2 2 2 C A B A z z AB AC z z i JJJG JJJG -3

Sajid mohammed sajidmadarissfr wwwmadarissfr 13 1 C A AC القطعة واسط هو M النقط مجموعة إذن MC MA أي z i z i zz zz 3 التمرين الخامس 3 ن المعرفة بما يلي n n u نعتبر المتتالية 1 21 2 n n n uu u -1 البرهان بالترجع u 1 حسب معطيات التمرين 0 لدينا n 0 1 n nnu من حيث 0 نفترض أنه توجد رتبة لدينا 0 0 0 1 1 2 2 2 1 1 1 n n n n nnu nn u nn u nnu 1 فإن وعلية n n u -2 أ- 1 1 1 2 2 2 1 2 n n n n n n vu u u v إذن n n v و 2 أساسها هندسية متتالية 0 0 v u 1 1 n الحد العام 2 n n v ب- 1 1 1 ln ln 1 ln 1 2 11 ln 1 2 1 ln 1 ln 2 nn n n n n n n n n n ww v v u u u u u u إذن n n w و ln 2 أساسها حسابية متتالية 0 0 w v ln 0 ln 2 ln 2 العام الحد n n n wn ج-
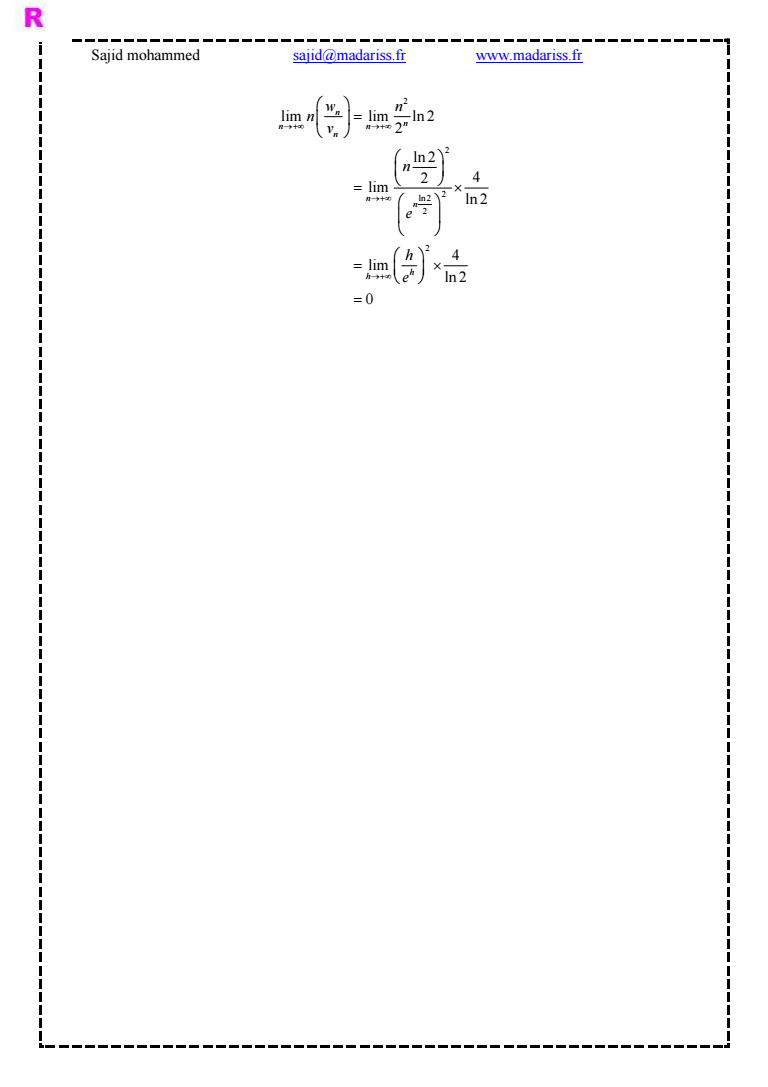
Sajid mohammed sajidmadarissfr wwwmadarissfr 2 2 2 ln 2 2 2 lim lim ln 2 2 ln 2 2 4 lim ln 2 4 lim ln 2 n n n n n n n h h w n n v n e h e
1 200825 3 7 ن 35 05 1 1 1 6 نقط 075 075 05 05 1 1 1 05 W 1 أ- بين أن 2 2 32 1 1 2 1 1 1 x x x x x x ب- استنتج قيمة التكامل 2 1 2 32 1 x x dx x I 2 باستعمال المكاملة بالأجزاء أحسب التكامل التالي 1 x J xe dx 3 أحسب التكامل 1 1 ln e e K x dx x W نضع المجموعة من z لكل 3 2 P z z iz iz i 8 3 25 24 75 التالية المعادلة المجموعة في حل 1 2 E z z 8 25 0 z صرفا يجب تحديده 2 0 بين أن المعادلة P z 0 تقبل حلا تخيليا بحيث b و a الحقيقيين العددين حدد 3 2 z P z z i z az b 3 و D التي ألحاقها على النقط A و B و 4 JG JG C نعتبر في المستوى العقدي المنسوب إلى معلم متعامد ممنظم Ouv A 1 2 هي التوالي 4 3 و z i B 3 و z i C z i D 4 3 و z i و D أ- مثل النقط A و B و C 1 ب- بين أن 5 C A D A z z i z z 2 و أن 3 C B D B z z i z z ج- استنتج طبيعة المثلثين ACD و BCD محددا شعاعها ولحق مرآزها و D تنتمي إلى دائرة د- بين أن النقط A و B و C حدد لحق النقطة E صورة النقطة C بالإزاحة 5 JJJJG t نعتبر الإزاحة t التي متجهتها AD

2 ن 105 05 1 15 1 05 1 1 05 1 075 075 1 W لتكن f الدالة العددية المعرفة على بما يلي 3 2 ln 1 0 4 3 0 fx x x fx xx x x lt JG JG المنحنى الممثل للدالة f في المستوى P المنسوب إلى معلم متعامد ممنظم Cf Oi j وليكن 1 أ - بين أن f متصلة في النقطة 0 ب- بين أن الدالة f قابلة للإشتقاق في النقطة 0 نذآر بأن ln 1 lim 1 x t t و 1 وتزايدية على المجال 2 01 بين أن الدالة تناقصية على آل من المجالين 0 3 أ- أحسب النهايتين التاليتين lim x f x lim و x f x 3 3ln ln 1 ب- تحقق من أن 0 fx x x x x x x Cf ج- أدرس الفرعين اللانهائيين للمنحنى 4 Cf أنشئ المنحنى 5 ليكن h قصور الدالة f على المجال 0 معرفة على مجال J يتم تحديده 1 h أ- بين أن h تقبل دالة عكسية لكل x من المجال 1 h x J ب- حدد المعرفة بما يلي 6 n n u نعتبر المتتالية العددية 2 1 4 9 4 3 n nn n u u uu u n أن بالترجع بين -أ 4 1 9 n un تزايدية n u ب- بين أن المتتالية n متقاربة ثم أحسب نهايتها n u ج- استنتج أن المتتالية n

W 2BacSP amp 2BacSVT 2008 25 2008 25 W W لدینا x 1 ليكن -أ 1 2 2 1 2 2 11 2 3 2 2 1 11 2 1 11 1 1 x x x xx x x x x x xx ب- لدینا 2 1 1 1 2 0 0 0 2 32 1 21 ln 1 2 1 1 ln 2 x x dx x dx x x x x x 2 باستعمال المكاملة بالأجزاء نجد 11 1 1 00 0 0 x x xx J xe dx x e dx xe x e dx 1 1 1 1 11 0 0 1 2 1 x x J e e dx e e e e e 3 لنحدد إشارة ln x على المجال 1 e e لدینا باستعمال علاقة شال نحصل على ما یلي 1 1 1 1 1 ln ln e e x dx x dx x x 1 1 1 1 11 1 ln ln ln e e e e x dx x dx x dx xx x K 1 1 1 ln ln ln ln e e x x dx x x dx 1 2 2 1 1 1 1 11 ln ln 0 0 2 2 1 2 2 e e Kx x W نضع من z لكل 3 2 P z z iz iz i 8 3 25 24 75 التالية المعادلة المجموعة في لنحل 1 2 E z z 8 25 0 لدینا 2 2 2 هما مترافقين عقدیين حلين E للمعادلة إذن b ac i 4 1 25 16 25 9 3 1 4 3 b i z i a 2 4 3 و b i z i a ومنه فإن مجموعة حلول المعادلة E هي Si i 43 43 ليكن 2 0 إذن P z 0 للمعادلة صرفا تخيليا حلا y بحيث z iy - 1 -

W 2BacSP amp 2BacSVT 2008 25 3 2 0 00 0 3 2 2 32 2 3 2 3 2 3 2 0 8 3 25 24 75 0 8 3 25 24 75 0 8 24 3 25 75 0 8 24 0 3 25 75 0 8 30 3 25 75 0 0 3 3 25 75 0 0 3 Pz z iz iz i iy i iy i iy i y yiy y y y y yy y y y yy y y أو y yy y Pz y z 0 3i هو حل تخيلي صرف للمعادلة P z 0 وبالتالي فإن لدینا 3 z 3i على القسمة تقبل P z إذن P z للحدودیة جدر z 0 3i طريقة 1 القسمة الأقليدية ومنه نستنتج أن a 8 و b 25 طريقة 2 تكون حدوديتان مختصرتان متساويتين إذا وفقط إذا آانت معاملات الحدود من نفس الدرجة متساوية 2 32 2 3 2 2 3 333 3 33 3 83 3 25 24 3 75 8 3 25 z z i z az b z z az bz iz aiz bi z z a i z b ai z bi ai i b ai i bi i a z z i z az b b P P P P نعتبر النقط A و B و C و D التي ألحاقها على 4 JG JG في المستوى العقدي P المنسوب إلى معلم متعامد ممنظم ومباشر Ouv 1 2 هي التوالي A 4 3 و z i B z i D 4 3 و z i C 3 و z i أ- تمثيل النقط A و B و C و D في المستوى العقدي P - 2 -
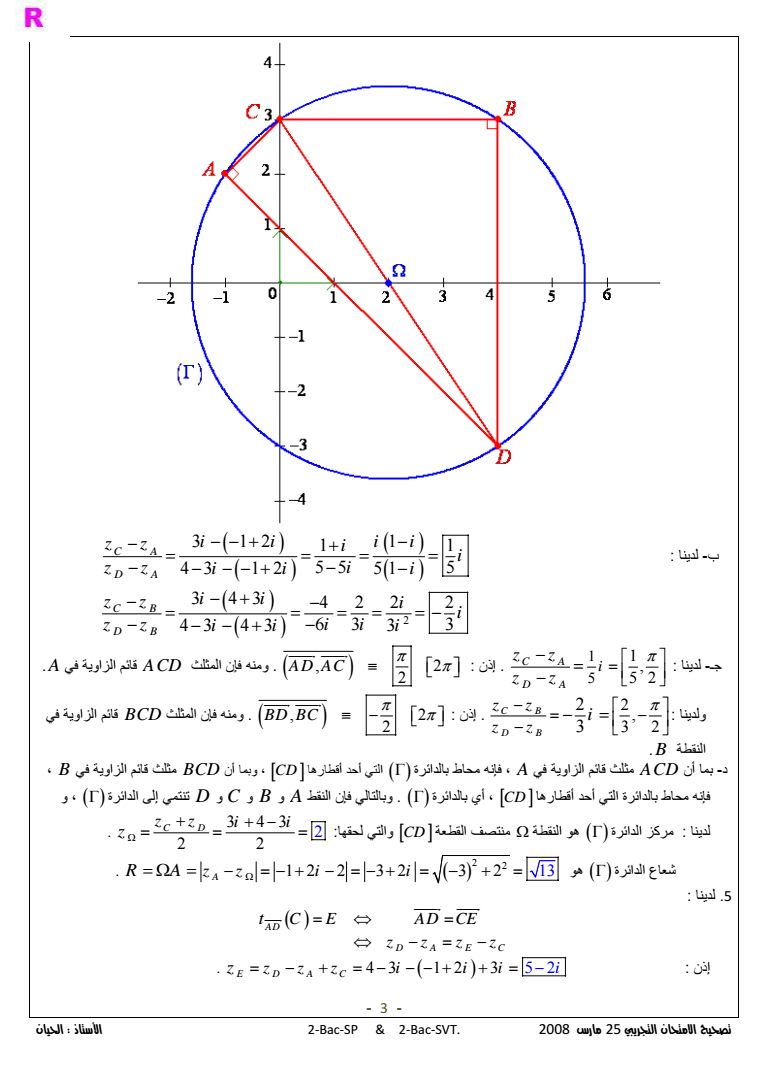
W 2BacSP amp 2BacSVT 2008 25 ب- لدینا 3 12 1 1 1 4 3 1 2 51 55 5 C A D A z z i i ii i i zz i ii i 2 3 43 422 2 43 43 63 3 3 C B D B z z i i i i zz ii i i i 1 ج- لدینا 5 1 5 2 C A D A i z z z z 2 إذن 2 AD AC JJJJG JJJJG A في الزاویة قائم ACD المثلث فإن ومنه 2 ولدینا 3 2 2 3 C B D B z z z z i 2 إذن 2 BD BC JJJJG JJJJG في الزاویة قائم BCD المثلث فإن ومنه النقطة B د- بما أن ACD مثلث قائم الزاویة في A فإنه محاط بالدائرة التي أحد أقطارها CD وبما أن BCD مثلث قائم الزاویة في B فإنه محاط بالدائرة التي أحد أقطارها CD أي بالدائرة وبالتالي فإن النقط A و B و C و D تنتمي إلى الدائرة و 3 3 2 4 لدینا مرآز الدائرة هو النقطة منتصف القطعة CD والتي لحقها 2 2 C D z z i i z هو الدائرة شعاع 2 2 12 2 32 2 3 13 A R A zz i i 5 لدینا AD D E A C C E AD CE zzzz t JJJJJG JJJJG JJJJG 4 3 3 1 2 5 2 إذن E D A C z zzz i i i i - 3 -

W 2BacSP amp 2BacSVT 2008 25 W لتكن f الدالة العددیة المعرفة بما یلي 3 2 ln 1 0 4 3 0 fx x x fx xx x x lt G JG المنحنى الممثل للدالة f في المستوى P المنسوب إلى معلم متعامد ممنظم Cf Oi j وليكن 1 2 أ- لدینا 0 0 lim lim 43 0 x x fx xx x f و 3 0 0 lim lim ln 1 ln1 0 0 x x f x xf إذن 0 0 lim lim 0 x x fx fx f ومنه فإن f دالة متصلة في النقطة 0 2 ب- لدینا 000 0 4 3 4 30 lim lim lim xxx fx f xx x x x x x d f إذن f قابلة للإشتقاق على اليمين في 0 و 0 0 نضع 3 إذن t x 0 0 x t ومنه فإن 6 3 3 2 2 3 3 0 00 0 ln 1 ln 1 0 ln 1 lim lim lim lim 0 x xx t 0 x x fx f t x t xx t x g f إذن f قابلة للإشتقاق على اليسار في 0 و 0 0 0 00 أن وبما g d f 0 0 ولدینا 0 النقطة في للإشتقاق قابلة f فإن f f x 0 ليكن 2 لدینا 2 3 3 3 3 1 ln 1 1 3 0 1 x x x f x x x 2 gt لأن و lt 3 0 x 3 1 0 gt x إذن f دالة تناقصية على المجال 0 x 0 ليكن لدینا 2 1 4 3 4 64 6 2 x xx x x x x x x x x x x f 2 4 6 1 1 6 6 6 1 x x x x x xx x x x f x هي إشارة 1x ولدینا ومنه فإن إشارة f x على المجال 0 و تزايدية على المجال 01 إذن f دالة تناقصية على المجال 1 لدینا -أ 3 2 lim lim lim 4 3 43 xx x fx xx x xx x نضع 3 إذن t x 1 x t 6 فإن ومنه 3 lim lim lim ln 1 ln xt t fx x t x 0 ليكن -ب لدینا 3 3 3 33 ln 1 ln ln 1 ln ln 1 ln 3 x x x x x x x xx x 3 3 3 ln 1 x x ln 1 x f x x x x - 4 -
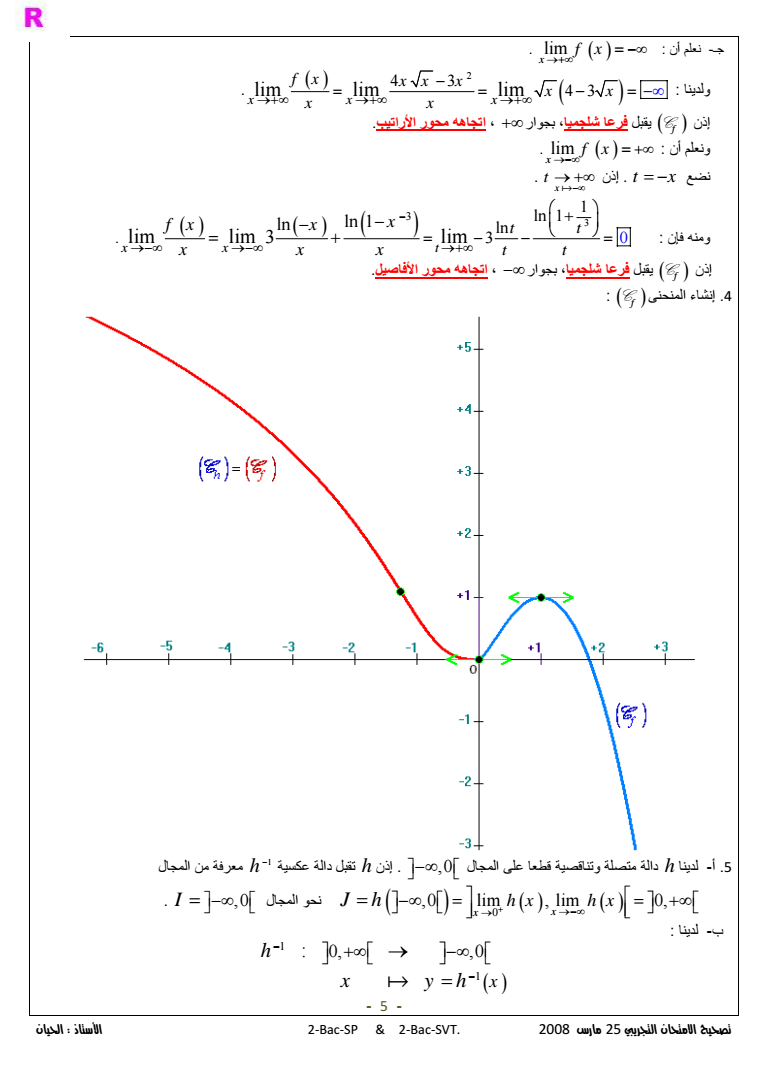
W 2BacSP amp 2BacSVT 2008 25 lim أن نعلم -ج x f x ولدینا 2 4 3 lim lim lim 4 3 xx x f x xx x x x x x یقبل فرعا شلجميا بجوار اتجاهه محور الأراتيب Cf إذن lim أن ونعلم x f x إذن t x نضع x t 6 3 3 ومنه فإن 1 n 0 ln 1 l 3 ln ln 1 lim lim lim 3 x x t t t t t fx x x x x x یقبل فرعا شلجميا بجوار اتجاهه محور الأفاصيل Cf إذن 4 Cf إنشاء المنحنى معرفة من المجال 1 h إذن h تقبل دالة عكسية 5 أ- لدینا h دالة متصلة وتناقصية قطعا على المجال 0 0 0 lim lim 0 x x J h hx hx نحو المجال I 0 ب- لدینا 1 1 0 0 x h x yh 6 - 5 -

W 2BacSP amp 2BacSVT 2008 25 x 0 ليكن بحيث y 0 و 1 y h x x بدلالة تحدیده ینبغي 1 3 3 3 3 3 3 1 3 ln 1 1 1 1 1 1 0 1 x x x x x x y h x hy x y x y e y e y e y e ye y yhx y e lt فإن وبالتالي 1 3 0 1 x x hx e المعرفة آما یلي 6 n n u نعتبر المتتالية العددیة 2 1 4 9 43 n nn n n f u u u uu u n 0 أ- من أجل n 0 لدینا 4 9 إذن u 0 4 1 9 u أن نفترض n ليكن 4 1 9 un 1 نبين أن 4 1 9 n u 4 1 لدینا f تزایدیة على المجال 9 إدن 1 1 4 48 1 9 81 4 4 1 11 9 9 n n n n u fff u u u 48 لأن 81 4 9 4 1 وبالتالي فإن 9 n un 2 ب- ليكن n لدینا 1 n nn n n n n n 4 3 4 31 n u u uu u u u u u 3 3 1 31 1 u uuu u u u u n nn n n n n n 1 nn n n 1 31 n u uu u u أن وبما 4 1 9 فإن un 0 unn n 1 11 0 u u و un و 2 1 23 3 13 12 3 uuu nnn إذن 1 n uu 0 n n فإن ومنه n n u تزایدیة متتالية - 6 -

W 2BacSP amp 2BacSVT 2008 25 طريقة 2 البرهان بالترجع 0 لدینا n 0 أجل من 9 4 9 1 0 و u 4 48 9 81 u u f f إذن u u 1 0 u u n1 n أن نفترض n ليكن 9 أن ونبين u u n n 2 1 4 1 نعلم أن f تزایدیة على المجال 9 وأن 4 1 9 n u n إذن 1 1 2 1 n n n n n n uu u u f f u u n u u n1 n فإن وبالتالي 9 متتالية تزایدیة n n u وعليه فإن متتالية تزایدیة ومكبورة بالعدد 1 فإنها متقاربة وبما أن n n u ج- بما أن المجال على متصلة f 9 4 1 9 f 9 4 1 متصلة وتزایدیة قطعا على المجال 9 إذن 4 4 48 4 1 1 1 1 9 9 81 9 f f f 0 9 4 4 1 9 9 u n 9 n u l نهایتها متقاربة متتالية و l l f فإن 41 9 l أن وبما 41 9 l lim 1 n فإن وبالتالي l 1 فإن n u على محور الأفاصيل باستعمال البرنام n n u Archimde II plus تمثيل حدود المتتالية العددية باستعمال البرنام 39 10 Maple 8 إلى n n u حساب الحدود الثمانية الأولى للمتتالية العددية - 7 -
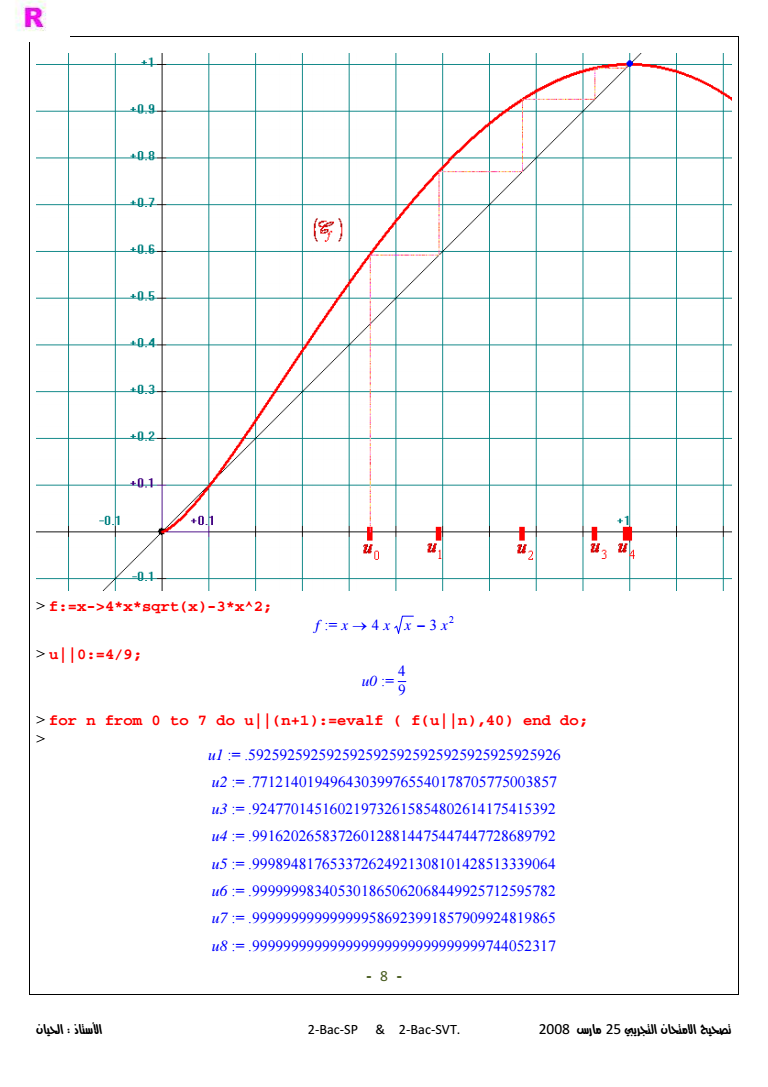
W 2BacSP amp 2BacSVT 2008 25 gt fx-gt4xsqrtx-3x2 gt u049 gt for n from 0 to 7 do un1evalf fun40 end do gt - 8 - f x 4 x x 3 x2 u0 4 9 u1 5925925925925925925925925925925925925926 u2 771214019496430399765540178705775003857 u3 924770145160219732615854802614175415392 u4 991620265837260128814475447447728689792 u5 999894817653372624921308101428513339064 u6 999999983405301865062068449925712595782 u7 999999999999999586923991857909924819865 u8 999999999999999999999999999999744052317

- 1 - ثانوية محمد رضا السلاوى الأستاذة نعيمة الزر هوني اآادير المستوى 2ب ع ت 2004 امتحان تجريبي مادة الرياضيات - - تمرين 1 o i j k G G G مباشر ممنظم متعامد لمعلم منسوب الفضاء C0-1-1 و B110 و A001 النقط نعتبر AB AC أحسب -أ -1 ب حدد معادلة ديكارتية للمستوى ABC 2 4 4 0 2 2 2 x y z x y المعادلة ذات S الفلكة نعتبر -2 أ- حدد مرآزها و شعاعها ب- بين أنABC و S يتقاطعان في دائرة محددا مرآزها و شعاعها تمرين 2 un un u 2 1 2 1 1 نعتبر المتتالية العددية un بحيث u5 و u4 و u3 و u2 أحسب 1 تكتب النتائج على الشكل r Q r 2 vn lnun ln 2 بحيث n v العددية المتتالية نعتبر -2 أ- بين أن n v هندسية محددا أساسها و حدها الأول ب- أحسب n v ثم un بدلالة n ج- أحسب un lim تمرين3 يحتوي صندوق على 3 آرات حمراء و3 آرات خضراء نسحب من الصندوق الكرة تلو الأخرى 1- أحسب عدد النتائج الممكنة - ليكن X 2 المتغير العشوائي الدى يساوي عدد الكرات الحمراء المسحوبة قبل سحب أول آرة خضراء أ- حدد قانون احتمال X و أحسب EX ب- مثل دالة التجرئ ثم أحسب VX و X

- 2 - تمرين4 ليكن عددا حقيقيا R 2 cos 2 0 2 1 2 E z z المعادلة C في حل -1 - المستوى منسوب الى معلم متعامد ممنظم مباشر o u v G G 2 لتكنA و B نقطتين لحقيهما 1 z و 2 z حدد لكي يكون المثلث متساوي أضلاع OAB مسالة نعتبر الدالة العددية f المعرفة على R آالتالي lt 1 ln 1 1 0 1 3 1 f x x x e x x x f x x 1- أ- بين أن متصلة في f 1 ب- أحسب نهايات عند محددات Df f 2 أدرس الفروع اللانهائية ل C f منحى f 3- أ- بين أن قابلة للاشتقاق في f 1 ب- أدرس تغيرات fثم أعط جدول تغيرات f 4- أ- حدد نقط انعطاف C f ادا آان x 1 ب- أنشئ C f 5- أ- بين أن h قصور f على المجال I 1 تقابل من نحو مجال يتم تحديده I 1 h x حدد -ب e I x dx 1 3 ln و e I x dx 1 6- أ- أحسب باستعمال مكاملة بالإجراء 2 ln ب- أحسب مساحة الحيز الذي يحده C f ومحور الأفاصيل والمستقيمان D x e و D x 1

- 3 - عناصر الإجابة تمرين 1 321 AB AC -أ -1 ABC 3x 2y z 1 0 -ب 120 و r 1 -أ -2 7 14 d dABC -ب d lt1 ادن S ABC C H R 7 5 R و 7 1 7 12 7 11 H تمرين2 - 1 2 1 2 4 3 3 8 7 4 16 15 5 u 2 u 2 u 2 u 2 2- ا- v1 ln 2 و 2 1 q n n v v 2 1 1 ب- 1 ln 2 2 1 2 1 lim 2 2 ln 2 1 n n n n u u e v n تمرين 3 Card 720 6 الممكنة النتائج عدد -1 X 0123 -أ - 2 2 1 6 5 0 10 3 6 4 1 20 3 2 2 1 3 1 3 1 3 1 3 A p X A A p X p X p X 075 20 15 EX 5 7 4 3 80 63 V X X -ب

- 4 - تمرين4 2 2 1 2 2 2 sin z z i -1 2 arg 2 3 2 2 1 z z -2 2 2 6 z1 z 2 أي مسالة 1- أ - f متصلة في 1 lim 0 lim lim lim 0 0 f x f x f x f x -ب بجوار أفقي مقارب D y 0 - 2 x 0 مقارب عمودي C f يقبل فرعا شلمجيا باتجاه محور الأفاصيل بجوار 0 f g x f d x 1 في للاشتقاق قابلةf 3 - أ - ب - 1 3ln 1 1 2 1 2 gt lt x x x f x e x x x f x x

- 5 - ln 2 3ln 2 x x x f x - 4 11 7 H1 H2 e الانعطاف نقطتي - أ - h 5 متصلة و تناقصية قطعا على I 1 ادن h تقابل من نحو 1 I 3 1 1 x f x e - ب J e 2 K 6 2e -أ -6 A 3e 74a منه و 1 ln 3 7 1 3 x dx e e ب- سلم التنقيط نقطة 05 -ب نقطة 05 -أ 1 1تمرين 2 أ- 05 نقطة ب- 1 نقطة نقطة 05 1 2تمرين 2 أ- 1 نقطة ب- 05 نقطة ج 05 نقطة نقطة 1 1 3تمرين 2 أ- 15 نقطة ب- 1 نقطة نقطة 15 2 ة نقطة 1 1 4تمرين مسالة 1 أ- 05 نقطة ب- 1 نقطة نقطة 1 2 3 أ- 1 نقطة ب- 15 نقطة 4 أ- 05 نقطة ب- 1 نقطة نقطة 05 -ب نقطة 05 -أ 5 6 أ-1 نقطة ب- 1 نقطة

أكاديمية مراكش تانسيفت الحوز نيابة شيشاوة مجاط ثانوية الخوارزمي التأهيلية الامتحان التجريبي لنيل شهادة البكالوريا دورة أبريل 2007 المادة الرياضيات الشعبة علوم تجريبية مدة الإنجاز 3 ساعات المعامل 7 1 2 يسمح باستعمال الآلة غير قابلة للبرمجة التمرين الأول 25ن في الفضاء المنسوب إلى معلم متعامد ممنظم A-2 2 -4 النقطتين نعتبر o i j k x - y z 2 0 معادلته الذي P المستوى و B4 -4 2 و 1 حدد معادلة ديكارتية للفلكة S التي أحد أقطارها AB ثم حدد شعاعها r و مركزها 1 Wن 2 حدد معادلة المستوى Q المماس للفلكة Sفي النقطة05 Aن 3 أحسب dW P ثم استنتج أن المستوى P يقطع الفلكة S وفق دائرة C حدد مركزها 1 Hن وشعاعها R التمرين الثاني 35ن 2 3 23 3 0 المعادلة في نعتبر 2 E z - -i z -i 1ن 1 حل في المعادلة E ن05 v 3 - 3 i و u 3 i العددين نعتبر 2 أ حدد الشكل المثلثي للعددين u و v ب أحس 025ن ب 2000 2 u ن075 Dv و Cv و B-u و Au النقط نعتبر 3 أ حدد الشكل الجبري للعدد u v u v - - واستنتج أن النقط A وC وD مستقيمية ن075 ب تحقق أن 2 1 i 3 v u v u - - استنتج قياس الزاوية CA CB ج استنتج طبيعة المثل 025 ABCن ث التمرين الثالث 3ن نعتبر صندوقين U و V الصندوق U يحتوي على 5 كرات بيضاء و 3 سوداء الصندوق V يحتوي على 3 كرات بيضاء وكرتين سوداويتين وكرة حمراء 1 نسحب عشوائيا بالتتابع وبدون إحلال كرتين من الصندوق U ونسحب كرة من الصندوق V أ ما هو احتمال الحصول على 3 كرات من نفس اللون 05ن ما هو احتمال الحصول على كرة بي 05ن ب ضاء فقط المتغير العشوائي الذي يربط كل إمكانية بعدد الكرات البيضاء ال 1ن ج ليكن X مسحوبة حدد قانون احتمال X نكرر الت 5 مرات متتالية 1ن 2 جربة السابقة ما هو احتمال الحصول على 3 كرات من نفس اللون 3 مرات بالضبط

أكاديمية مراكش تانسيفت الحوز نيابة شيشاوة مجاط ثانوية الخوارزمي التأهيلية الامتحان التجريبي لنيل شهادة البكالوريا دورة أبريل 2007 المادة الرياضيات الشعبة علوم تجريبية مدة الإنجاز 3 ساعات المعامل 7 2 2 ن05 ن05 ن05 ن05 1ن 1ن 1ن ن075 1ن ن05 1ن ن05 ن05 ن075 1ن مسألة 11ن لتكن f الدالة العددية للمتغير الحقيقي المعرفة بما يلي - 3 - gt - 2 2 3 0 2 2 ln 2 1 0 f x e e x f x x x x x x x منحنى الدالة f في معلم متعامد ممنظم C f وليكن o i j الجزء الاول 1 أدرس اتصال الدالة f في 0 lim f x حدد أ 2 x و lim f x x - C f ل الانهائية الفروع أدرس ب 3 أ أدرس قابلية اشتقاق الدالة f على يمين وعلى يسار 0 وأول النتيجتين هندسيا ب بين أن lt - gt 2 1 4 ln 0 2 x e e f x f x x x x x x ج استنتج تغيرات الدالة f وأعط جدول تغيرات الدالة f 4 أ بين أن lt gt 2 1 4 ln 4 0 2 x e e f x f x x x x x ب أدرس تقعر C f واستنتج نقط انعطافه أنشئ 5 C f I - 0 على f الدالة قصور g ليكن 6 أ بين أن g تقابل من I نحو مجال J حدده ب حدد 1 g x - J من x لكل C منحنى الدالة g ج أنشئ 1- g في نفس المعلم 1 - o i j الجزء الثاني المعرفة u n بما يلي نعتبر المتتالية quot 1 ln 2 3 1 n n u n N u f u quot n N 1 p u n p 2 أن بين 1 تناقصية قطعا 2 u n بين أن متقاربة وحدد نهايتها 3 u n استنتج أن المتتالية

أكاديمية مراكش تانسيفت الحوز نيابة شيشاوة مجاط ثانوية الخوارزمي التأهيلية الامتحان التجريبي لنيل شهادة البكالوريا دورة أبريل 2007 المادة الرياضيات الشعبة علوم تجريبية مدة الإنجاز 3 ساعات المعامل 7 1 2 يسمح باستعمال الآلة غير قابلة للبرمجة التمرين الأول 25ن في الفضاء المنسوب إلى معلم متعامد ممنظم A-2 2 -4 النقطتين نعتبر o i j k x - y z 2 0 معادلته الذي P المستوى و B4 -4 2 و 1 حدد معادلة ديكارتية للفلكة S التي أحد أقطارها AB ثم حدد شعاعها r و مركزها 1 Wن 2 حدد معادلة المستوى Q المماس للفلكة Sفي النقطة05 Aن 3 أحسب dW P ثم استنتج أن المستوى P يقطع الفلكة S وفق دائرة C حدد مركزها 1 Hن وشعاعها R التمرين الثاني 35ن 2 3 23 3 0 المعادلة في نعتبر 2 E z - -i z -i 1ن 1 حل في المعادلة E ن05 v 3 - 3 i و u 3 i العددين نعتبر 2 أ حدد الشكل المثلثي للعددين u و v ب أحس 025ن ب 2000 2 u ن075 Dv و Cv و B-u و Au النقط نعتبر 3 أ حدد الشكل الجبري للعدد u v u v - - واستنتج أن النقط A وC وD مستقيمية ن075 ب تحقق أن 2 1 i 3 v u v u - - استنتج قياس الزاوية CA CB ج استنتج طبيعة المثل 025 ABCن ث التمرين الثالث 3ن نعتبر صندوقين U و V الصندوق U يحتوي على 5 كرات بيضاء و 3 سوداء الصندوق V يحتوي على 3 كرات بيضاء وكرتين سوداويتين وكرة حمراء 1 نسحب عشوائيا بالتتابع وبدون إحلال كرتين من الصندوق U ونسحب كرة من الصندوق V أ ما هو احتمال الحصول على 3 كرات من نفس اللون 05ن ما هو احتمال الحصول على كرة بي 05ن ب ضاء فقط المتغير العشوائي الذي يربط كل إمكانية بعدد الكرات البيضاء ال 1ن ج ليكن X مسحوبة حدد قانون احتمال X نكرر الت 5 مرات متتالية 1ن 2 جربة السابقة ما هو احتمال الحصول على 3 كرات من نفس اللون 3 مرات بالضبط

أكاديمية مراكش تانسيفت الحوز نيابة شيشاوة مجاط ثانوية الخوارزمي التأهيلية الامتحان التجريبي لنيل شهادة البكالوريا دورة أبريل 2007 المادة الرياضيات الشعبة علوم تجريبية مدة الإنجاز 3 ساعات المعامل 7 2 2 ن05 ن05 ن05 ن05 1ن 1ن 1ن ن075 1ن ن05 1ن ن05 ن05 ن075 1ن مسألة 11ن لتكن f الدالة العددية للمتغير الحقيقي المعرفة بما يلي - 3 - gt - 2 2 3 0 2 2 ln 2 1 0 f x e e x f x x x x x x x منحنى الدالة f في معلم متعامد ممنظم C f وليكن o i j الجزء الاول 1 أدرس اتصال الدالة f في 0 lim f x حدد أ 2 x و lim f x x - C f ل الانهائية الفروع أدرس ب 3 أ أدرس قابلية اشتقاق الدالة f على يمين وعلى يسار 0 وأول النتيجتين هندسيا ب بين أن lt - gt 2 1 4 ln 0 2 x e e f x f x x x x x x ج استنتج تغيرات الدالة f وأعط جدول تغيرات الدالة f 4 أ بين أن lt gt 2 1 4 ln 4 0 2 x e e f x f x x x x x ب أدرس تقعر C f واستنتج نقط انعطافه أنشئ 5 C f I - 0 على f الدالة قصور g ليكن 6 أ بين أن g تقابل من I نحو مجال J حدده ب حدد 1 g x - J من x لكل C منحنى الدالة g ج أنشئ 1- g في نفس المعلم 1 - o i j الجزء الثاني المعرفة u n بما يلي نعتبر المتتالية quot 1 ln 2 3 1 n n u n N u f u quot n N 1 p u n p 2 أن بين 1 تناقصية قطعا 2 u n بين أن متقاربة وحدد نهايتها 3 u n استنتج أن المتتالية
Nouro Nourex
أرسلت .
- الملفات : الملفات.
- المستوى : الثانية باكالوريا.
- المادة : الرياضيات.
كلمات مفتاحية :
الامتحانات التجريبية
الامتحانات التجريبية