الامتحان الوطني لسنة 2012 للرياضيات correction

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 1 sur 17 www arabmathsiftfr ذ سعيد الصديق ثاالشابي التأهيلية تارودانت حساب و 2 2 تصحيح الإمتحان الوطني لمادة الرياضيات السنة الثانية علوم رياضية يونيو 2012 التمرين الأول I

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 2 sur 17 www arabmathsiftfr A تقبل مقلوبا لدينا 2 و إذن المصفوفة A تقبل مقلوبا تحديد مقلوب A لدينا إذن ليكن yو x من R لدينا قانون تركيب داخلي في I ليكن bو a من لدينا 1 lt و 1 lt 2 gt 1 و 2 gt 1 2 2 gt 0 II

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 3 sur 17 www arabmathsiftfr 2 2 gt 1 22 2 2 gt 1 22 2 2 gt 1 gt 1 وبالتالي R نحو أ - - تشاكل تقابلي من - تشاكل ليكن bو a من R 0 0 لدينا وبالتالي - تشاكل من R نحو تقابل من R نحو I ليكن y من I لنحل في R 2 -3 المعادلة 2 -3 2 3 22 3 قانون تركيب داخلي في I

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 4 sur 17 www arabmathsiftfr 3 22 R المعادلة 2 -3 تقبل حلا وحيدا في R إذن تقابل من R نحو I وبالتالي ب بنية بما أن R زمرة تبادلية و - تشاكل تقابلي من R نحو فإن ج 5 زمرة جزئية من لدينا 5 لدينو ا 5 إذن 5 ليكن yو x من 5 إذن يوجد و m n من Z بحيث و إذن lt -gt - - gt - lt - gt - R نحو - تشاكل تقابلي من زمرة تبادلية

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 5 sur 17 www arabmathsiftfr - gt A - gt 5 وبالتالي تحديد B و B حلي المعادلة C مميز المعادلة C هو E E E 2 E E 2 E2 إذن F E E E E E E E E E F E E E E E E E E BB 2G أ- BB G G لدينا G 2G ب - BB عدد حقيقي HIJ L M N L O IJBB L يكافئ حقيقي عدد BB لدينا زمرة جزئية من Q التمرين الثاني I و

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 6 sur 17 www arabmathsiftfr HIJ E L HIJ IJE L HIJ L L HIJ R M N R O ES F ES FT ES مستقيمية M و D A و أ - و D A و M مستقيمية يكافئ U U ES R U U VS TTTTT A U U ES UW UWES U U ES F FT ES FT F ES ES F ES FT ES ES F ES FT X Z - ب لدينا X Z يكافئ a TTTTTTTTTTTTTT R R IJ F ES R R F ES ER F VS A TTTTTTTT F ES FT ES F ES ES F ES FT II ST S
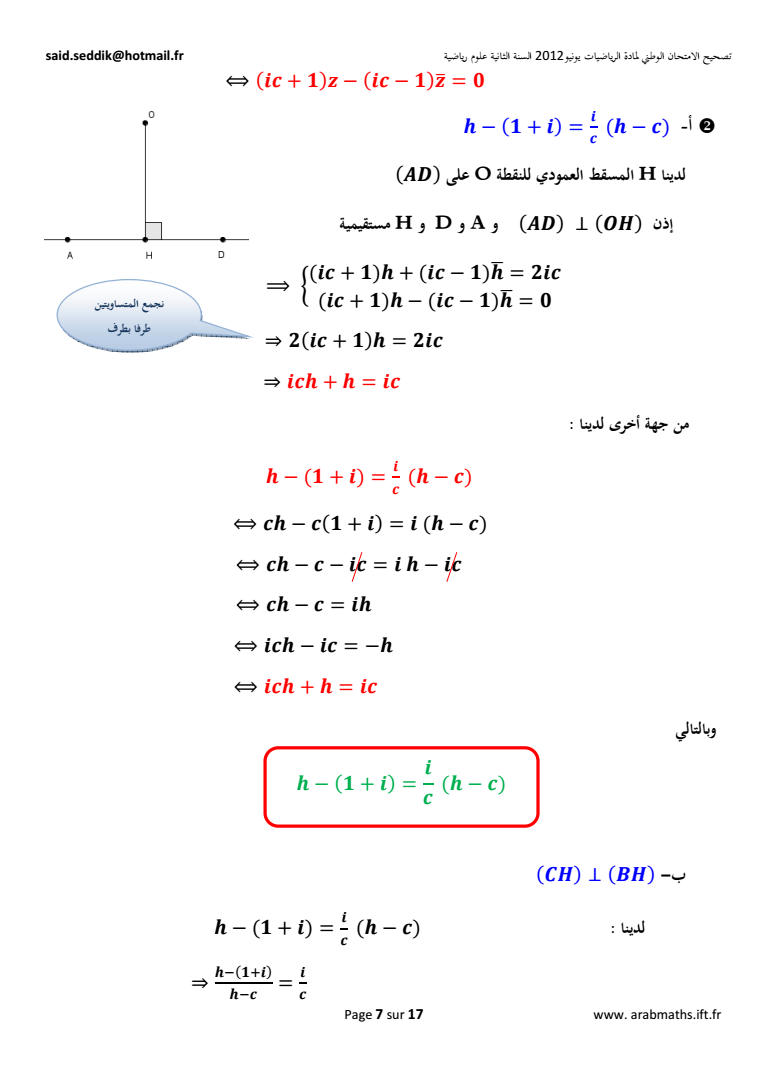
تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 7 sur 17 www arabmathsiftfr ES F ES FT b E أ - E S b S لدينا H المسقط العمودي للنقطة O على X إذن X Zc و و D A و H مستقيمية eES b ES bW ES ES b ES bW ES b ES ESb b ES من جهة أخرى لدينا b E E S b S Sb S E E b S Sb S ES E b ES Sb S Eb ESb ES b ESb b ES وبالتالي gc hc - ب b E لدينا E S b S b E b S E S b E E S b S نجمع المتساويتين طرفا بطرف

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 8 sur 17 www arabmathsiftfr IJ b E b S A R R ij kj TTTTTTTTTTTTT R R gc hc -أ l لدينا حسب خوارزمية إقليدس l l l l إذن l بما أن 13 تقسم 52 فإن المعادلة C تقبل حلولا في Z ب - حل المعادلة C في Z ليكن الزوج حلا للمعادلة C في Z إ ذن l e ك Gauss فإن o بما أن حسب مبرهنة وص pp Z و p التمرين الثالث

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 9 sur 17 www arabmathsiftfr p و p p Z p و p p Z عكسيا لدينا p p p p و بالتالي p N gtu 5 عدد أولي حسب مبرهنة فيرما Fermat لدينا lt بما أن lt فإن lt إذن lt p p مهما يكن k من N و بالتالي lt p N u gt 3 gt2 -أ p N 3 2 u إذن 3 2 لدينا gt3 2 gt 3 gt2 gt 3 gt2 ب - N gt3 gt2 العددان lt و lt 3 لهما نفس الزوجية إذن lt 2 3 gt2 عدد زوجي gt3 gt2 gt3 gt2 wC x p p p Z y

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 10 sur 17 www arabmathsiftfr 3 gt2 بما أن فإن lt gt و lt 3 2 لهما نفس رقم الوحدات في نظمة العد العشري الزوج حل للمعادلة C p Z p و p إذن p 3 2 gt3 gt2 أي العددان lt و lt 3 2 لهما نفس باقي القمة الإقليدية على 10 و بالتالي lt و lt 3 2 لهما نفس نفس رقم الوحدات في نظمة العد العشري zE zE و zE zE zE zE zE A بجوار -أ الفرع اللانهائي للمنحنى zE zE A A إذن بجوار ب - 2 3 مقارب مائل للمنحنى التمرين الرابع يقبل فرعا شلجميا في اتجاه محور الأراتيب بجوار

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 11 sur 17 www arabmathsiftfr zE لدينا zE A zE و X الوضع النسبي للمنحنى لدينا gt 0 وبالتالي تغيرات الدالة لدينا lt lt z z يوجد فوق X
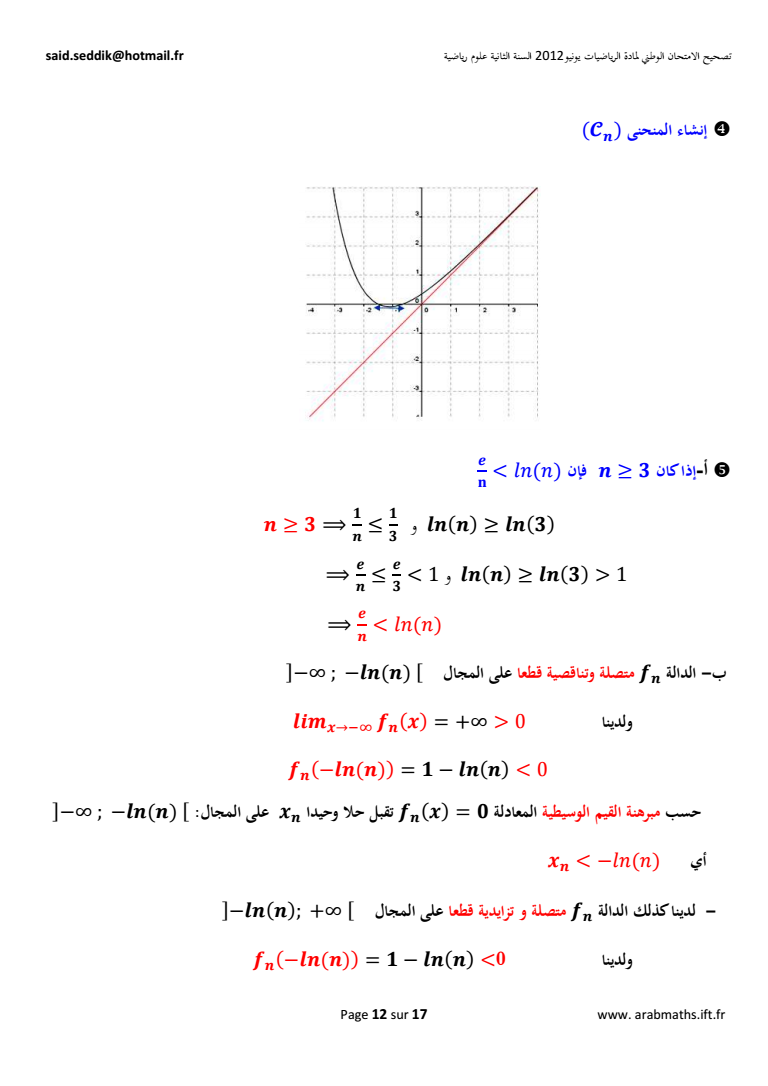
تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 12 sur 17 www arabmathsiftfr إنشاء المنحنى -أ إذا كان فإن gt lt و z z lt 1 و z z gt 1 lt ب - الدالة متصلة وتناقصية قطعا على المجال z zE ولدينا 0 lt z z lt 0 تقبل حلا وحيدا على المجال z حسب مبرهنة القيم الوسيطية المعادلة أي gt - لدينا كذلك الدالة متصلة و تزايدية قطعا على المجال z z z lt0 ولدينا

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 13 sur 17 www arabmathsiftfr zE gt 0 تقبل حلا وحيدا على المجال z حسب مبرهنة القيم الوسيطية المعادلة من جهة أخرى لدينا lt gt z O N z و لدينا gt 0 A A lt 0 إذن lt lt 0 وبالتالي تقبل بالضبط حلين و بحيث gt و المعادلة lt lt 0 -ج zE و zE لدينا gt و zE z إذن zE و لدينا zE و lt lt 0 إذن zE -أ g متصلة علي اليمين في 0 zE J zE z J ب - 3gt A gt3 3gt 3 1 1 3 3 lt 1 1 lt 0 lt 1

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 14 sur 17 www arabmathsiftfr بما أن فإنه يوجد حل للمعادلة J A J z z z z ج - zE z لدينا zE A بما أن g متصلة علي اليمين في 0 فإن zE J A J zE وبالتالي z zE J A لدينا التمرين الخامس

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 15 sur 17 www arabmathsiftfr - أ 2 لدينا A z z إذن z A z 2 ب - لدينا 2 2 2 - F متصلة على اليمين في 0 لدينا oe و zE إذن oezE

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 16 sur 17 www arabmathsiftfr نضع و gt إذن 2 و 2 إذن lt N 2 O 2 2 2 A 2 lt -أ A 2 لدينا 2 A 2 2 2 A 2 2 A 2 lt A 2 2 A 2 A 2 A 2 ب - lt 2 لدينا 2 2 A 2 2

تصحيح الامتحان الوطني لمادة الرياضيات يونيو2012 السنة الثانية علوم رياضية saidseddikhotmailfr Page 17 sur 17 www arabmathsiftfr 2 2 A 2 2 A 2 3 3 A 2 3 2 lt 2 ج - ليكن x من المجال الدالة oe z متصلة على المجال و متصلة على اليمين في 2 0 إذن F متصلة على و قابلة للاشتقاق على حسب مبرهنة التزايدات المنتهية فإنه يوجد عدد S من المجال بحيث lt S ولدينا lt S S2 lt S S من جهة أخرى 2 2 S 2 2 S 2 2 lt S 2 2 S -د لدينا zE 2 S إذن zE وبالتالي F قابلة للاشتقاق على اليمين في و 0 oe lt لا تنسونا من صالح دعائكم و مرحبا بملاحظاتكم
Basma El Khamlichi
أرسلت .
- الملفات : الملفات.
- المستوى : الثانية باكالوريا.
- المادة : الرياضيات.
كلمات مفتاحية :
الامتحان الوطني لسنة 2012 للرياضيات correction
الامتحان الوطني لسنة 2012 للرياضيات correction